Раздел: Документация
0 ... 84 85 86 87 88 89 90 ... 143 Из второго уравнения определяем р [1 + I — k, е] = (1/е,) (е) — р [/ — k, в] е, ,}. Из третьего уравнения получаем р[2-М — k,s] = (1/е,)№-2(8) — pU — k, е]е, 2 — р[1 +/ — k, е]е, !) или в сокращенной форме записи Р[2 + / — k, е] = (1/е/){4 2(е)—Sop[f+ / —/г, е]e, 2+j (8.82) По аналогии с (8.82) значение выходной величины в момент времени t = s + / — fe + e можно определить с помощью следующего рекуррентного соотношения [161: if5-1) P[s + / — k, е] = — dk-s{e)— SpIi + Z — fe, е]е, 5+Л (8.83) . Полученное выражение позволяет определить кривую переходного процесса не только в дискретные моменты квантования (при е = 0), но и в промежутках между ними, если придавать е значения от 0 до 1. С помощью этого выражения можно определять реакцию системы на воздействие произвольной формы. Для определения переходной функции системы на ее вход подают единичное ступенчатое воздействие, z-изображение которого z[l [n]} = z/(z— 1).(8.84) В этом случае z-изображение реакции (переходной функции) системы р (z, е) = К3 (г, е) z/(z — 1).(8.85) Пример 10. Рассчитать переходную функцию замкнутой импульсной системы автоматического сопровождения цели по дальности с двумя интеграторами (рис. 8.36), передаточная функция которой в замкнутом состоянии определяется выражением (8.73): Лз (Z, В) ■■ CgZ2 + qz + с„ где Ь2 (г) = ka + fe4e; h (е) = fe4 — k3 — kte; bB (e) = 0; c2=l; q = — (2 — ft3 — ft4); c0=l— k3. при следующих параметрах системы: ka = ktfTk,. = Л, = 0,84; fe4 = kByT*k2 = Tk2 = 0,6. z-Изображение переходной функции системы в соответствии с выражением (8.85) zb2 (е) z2 + bt (е) г г Ь2(е)г* + Ь, (e)z2rf3 (е) г» + d2 (е) z2 CaZ3 + {ct — c2) z2 + (cfl — ct) z — c0 e8z3 + e-jZ2 + exz + 262 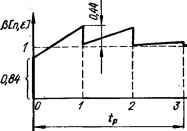 Рнс. 8.40. Кривая переходного процесса импульсной системы (рнс. 8.36), где da (е) = 6а (е) = kg + ft4e = 0,84 + 0,6е; d2 (е) = Ьх (е) = fe4 — k3 — V = 0,24 — 0,6е; е3 = с2 = 1; ea = ci — с2 = — 2 + fe3 + fe4— 1 = — 1,56; е* = с0 — ct = 1 — ka + (2 — ft3 — fe4) = 3 — 2ft3 — fe4 = 0,72; Co = — c„ = — (1 — fc3) = — 0,16. Для расчета переходной функции воспользуемся рекуррентным соотношением (8.83). Для рассматриваемого примера, как видно из выражения (8.86)," высшие показатели степеней знаменателя / н числителя k г-изображения переходной функции равны / = k = 3, поэтому рекуррентное соотношение примет вид PI*. е] = — {d3 s(e)- s-1л ■ £ PP. е]е3 !+г . Дискретные значения переходной функции системы в соответствии с последним выражением: р [0, е] = (1/е3) (в) = 0,84 + 0,6в; р [1, 8] = (1/е3) jda (е) - £ р [t, е] ез 1+1. = (1/е3) {da (е) - р [0, в] е8} - = — (0,24 + 0,6е) — (0,84 + 0,6е) (— 1,56) = 1,07 + О.ЗЗбв; р [2, е] = (1/ej) d2 (е) - р [I, е] ез 2+, = = (l/es) {dt (е) - р [0, 8] ех - р [1, е] е8} = = 0 — (0,84 + 0,6е) 0,72 + (1,07 + О.ЗЗбе) 1,56 = 1,07 + 0,09в. р [3, е] = (1/е3) jdo (е) - J] р [I, el еа н = = (1/еэ) {d0 (е) ~ Р [0, е] е0 - р [1, е] ех — р [2, е] еа} = «= 0 + (0,84 + 0,6е) 0,16 — (1,07 + О.ЗЗбе) 0,72 + (1,07 + 0,09е) 1,56 = 1,02 + 0,01 е; Р(4, е] = 1,00 + 0,01е; р [s, е] ss 1 при s > 4. Кривая переходного процесса, построенная по расчетным данным, изображена на рис. 8.40. Из рисунка видно, что перерегулирование о = (ДВ/Вуст) • 100 = = (0,44/1) 100 = 44 %, а время регулирования tp = (3...4) Т = 10... 15 с Косвенные методы оценки качества импульсных систем В теории импульсных систем, как и в теории систем непрерывного действия, для оценки качества процесса управления часто применяются косвенные методы, не требующие построения самого процесса управления. Оценка качества импульсной системы по степени устойчивости. Как установили при анализе устойчивости, переходная составляющая решения разностного уравнения замкнутой системы Рп [Н = A1/1 + A2zr2 + ... + Апггп, где z{ — t-й корень характеристического уравнения F3 (z) = c„z" + c-iz"-1 + •-• + с0 = 0. При подстановке вместо z его значения е переходная составляющая будет определяться выражением Рп И = Аг + А*" + ... + A„eV где q{ = а{ + /со — i-й корень характеристического уравнения з(?) = с„е»"+с„ 1е<<«-1>Н----+с0 = 0.(8.87) В устойчивой системе, переходный процесс которой имеет затухающий характер, действительные части всех корней q{ характеристического уравнения отрицательны. Быстрота затухания переходного процесса системы определяется наименьшей по абсолютной величине действительной частью корня а = min Re qc , называемой степенью ус- . тойчивости системы. В импульсной системе можно добиться бесконечной степени устойчивости, когда все корни характеристического уравнения (8.87) имеют действительные части, равные —оо. Бесконечная степень устойчивости имеет место, если выполняется условие с0 = <* = ■ • • = Сл-1 = 0.(8.88) Действительно, в этом случае F3 (q) = cnefn = 0, и поэтому должно выполняться условие e*n = e°"e±/<07 = 0, что возможно лишь при а = —оо. При бесконечной степени устойчивости переходный процесс в си стеме заканчивается за конечное время. В этом нетрудно убедиться" г-Изображение переходной функции системы в соответствии с выражениями ; (8.85) и (8.79) и учетом (8.88) равно 2 4 (е) гк + dfe , (е) г*"1 + • • • + d0 (е) Р(г, e) = K3(z, 8)- z— 1е,г = Р [0, 8],+ Р [1, ej г"1 + р [2, е] г~2 + 0 ... 84 85 86 87 88 89 90 ... 143 |












