Раздел: Документация
0 ... 83 84 85 86 87 88 89 ... 143 имели отрицательные вещественные части, необходимо и достаточно, чтобы при с„ > 0 все п определителей Гурвица, составленные из коэффициентов этого уравнения, были больше нуля, т. е. Д„>0, Д„ , >0.....At>0. Пример 9. Определить устойчивость импульсной системы автоматического сопровождения цели с двумя интеграторами (рис; 8.36), передаточная функция которой в замкнутом состоянии определяется выражением (8.73) Me) г* + &,(е) г л3 (г. е) =-—-■-, + Cjz + с0 где % = 1 — ks; cj = — (2 — ks — kt); = 1; /г3 = A„yTAi; Приняв знаменатель передаточной функции Ка (2, е) равным нулю, получим характеристическое уравнение замкнутой системы Fз (z) = c2z2 + CjZ + с0 = 0. Для получения преобразованного характеристического уравнения осуществим, подстановку г= (1 + ai)/(l — а>): 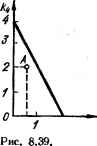 Облает*, устойчивости импульсной системы с двумя интеграторами. (1 + (1 — wf 1 -I- ву 1 — w + с0 = 0, или F3 (Ш) = cs (1 + vuf + Cl (1 + ш) (1 - ш) + с0 (1 - wf- = ; с2 + ce%w + taa,S + ci — с1ш8 + со — Со + = 4 + clw + со = 0, где = Cjj + ct + с„ = й4; с = 2 (са — с0) = 2£8; Главный определитель Гурвица 1 с, О : с2 — ci + со = 4 — 2*3 — а условие устойчивости при с2 = 4 — 2 — fe4 > 0 запишется следующими неравенствами: А1 = с=2й3>0; ~ Да = CpcJ = 2&Д, > 0. Поскольку коэффициенты системы кя и к} положительны, то условие устойчивости системы имеет вид 4 — 2k3 — й4 > 0. Из уравнения 4 — 2k3 — й4 = 0, определяющего границу устойчивости системы, можно на плоскости параметров к3 и й4 найти область устойчивости. Эта область ограничивается прямой й4 = 4 — 2k3, т. е. область устойчивости представляет собой прямоугольный треугольник с катетами к3 = 2, &t — 4 (рнс. 8.39). Если точка с координатами (fe3, &4) будет находиться внутри треугольника, то система устойчива. Например, точка А, соответствующая к3 = 0,5 и А4 = 2, находится внутри треугольника. Следовательно, система с такими коэффициентами устойчива. 8.8. Анализ качества импульсных САУ Поведение импульсной системы в переходном режиме характеризуется показателями качества — перерегулированием, временем регулирования, временем установления, числом колебаний. Показатели качества могут быть определены из кривой переходной функции системы, являющейся реакцией системы на единичное ступенчатое воздействие. Построение переходных процессов в замкнутой импульсной системе Кривая переходного процесса импульсной системы может быть определена с помощью различных методов: решением разностных уравнений (см. формулу (8.60)), нахождением дискретного изображения выходной величины системы и переходом от него к оригиналу, с помощью частотных методов. Рассмотрим метод определения выходной величины по ее дискретному изображению. Построение переходных процессов в замкнутой импульсной системе по их дискретным изображениям. Передаточная функция замкнутой импульсной системы, как известно (см. формулу 8.65), определяется выражением 1 + г-[Кр (г, 1) 2-(2,1) откуда изображение выходной величины системы: р (z, г) К3 (г, е) гГа (z, 1) = ; /У. 7 й z a (z> !> 1 + z 1Кр (г, 1) где г~ха (z, 1) — изображение входного сигнала, или для случая, когда сигнал, поступающий на импульсный элемент, не претерпевает скачков: Р (г, г) = К3 (z, в)а (г, 0) = {Кр (z, е)/[1 + Кр (г, 0)]} а (г, 0). Для определения реакции системы Р [п, е] (кривой переходного процесса) на данный входной сигнал необходимо выполнить обратное z-преобразование, т.е. найти оригинал функции по ее z-изображению. На практике нашли применение следующие методы определения оригинала функции по ее z-изображению: —непосредственное определение оригинала по таблицам преобразования. Применяется в случае, когда z-изображение имеет сравнительно простое выражение; —определение оригинала путем разложения z-изображения на элементарные дроби и нахождение по таблицам оригиналов, соответствующих этим элементарным дробям. Сумма составляющих оригиналов представляет собой искомый оригинал; —метод разложения z-изображения в степенной ряд по степеням z—1; этот метод рассмотрим более подробно. Определение переходных процессов методом разложения их з-изоб-ражений в степенной ряд. В общем случае z-изображение выходной величины системы можно представить в виде отношения полиномов „, . „ , , -1 ,* (в) «* +(8) Я*"1 + ... +d„(8) 6(z,e) = /C3(z,e)z а (г, 1) =-—- -■-,(8.78) e,z + e, ,z + ••• +е0 где k /. В соответствии с формулой (8.36) z-преобразования можно также записать: со p[z, е] =Z {p[n, е]} = S р[п, е]г~п =» = p[0,e] + p[l,e]z-1 +6[2,e]z-2+ ••• + p[n,e]z " +(8.79) Значения коэффициентов Р [и, е] степенного ряда при г~п соответствуют значениям выходной величины системы в дискретные моменты времени 7 = п + е. Поэтому для определения дискретных значений переходного процесса системы необходимо определить коэффициенты степенного ряда. Определить искомые коэффициенты через параметры системы и входное воздействие можно путем приравнивания правых частей выражений (8.78) и (8.79): dk(e)2k+dk 1(e)zk-1+ ■-■ +rf0(e) е + ент "•+<*> = p[0,e] + p[l,e]2-1+p[2,e]z-2+ dk (е) zk + dft , (e) z*-1 + • • • + d0 (e) = = (e,z< + e/ lZ- + - - - + e0) {P [0, 1] + p [1, e] ar> + • • •}. (8.80) Раскрыв скобки в правой часта выражения и приравнивая коэффициенты левой и правой частей при одинаковых степенях z, получим систему уравнении, из которой затем определим искомые ординаты. Как отмечалось, k I. Обозначим I — k = п0, откуда k — I — п0, где По — порядковый номер ординаты, с которого значения ординат отличны от нуля, а ординаты р [0, е] = ... = Р 17 — k — 1, е] = 0. С учетом данного замечания, приравнивая коэффициенты правой и левой частей выражения (8.80) при одинаковых степенях г, получим следующую систему уравнений: при z° dk (е) = Р [/ — k, е] е;; при г-1 dk-i (в) = р [I — k, е] е/ ! + Р [1 + / — k, в\ е,; при г-2 dk-2 (е) = Р U — k, в] ei-2 + Р [1 + I — К в] е/ ! + + р [2 + / — К е]е, и т. д., из которой можно определить дискретные значения кривой переходного процесса системы. Из первого уравнения находим дискретное значение величины в момент времени 1=1 — k + в: fill — k, в] = dk (е)/е,. откуда (8.81) 0 ... 83 84 85 86 87 88 89 ... 143 |












