Раздел: Документация

0 ... 85 86 87 88 89 90 91 ... 143

Рис. 8.41. Монотонная ступенчатая переходная функция системы:

о — соответствующая переходной функции системы: б — соответствующая отклонению переходной функции от ее предельного значения.

откуда

d*(e)z*+4i i(e)«fc-I+ ... +d„(e) = = е/г{р[0,е]+ ... +р[/-*-1,е]г-«-*-1> + -f P[/-ft, е]г-«,-*>+ ...}.

Учитывая, что k < / и Р [0] = ... = В [I — k — 1] = = 0, получим

p[/-ft, е] = dk (е)/е,; P[l+/-fc, е] = йЛ 1(е)/е<;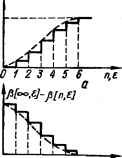

0f23456 л£ 0~ • - *

р [ft + / - ft, 8] = р [/, е] = d„ (е)/е,; Р[т, е] = 0 при т>1,

т. е. переходный процесс системы прн бесконечной степени устойчивости заканчивается за конечное число периодов.

Интегральные оценки качества. Если переходная функция системы имеет монотонный характер (рис. 8.41, а), то для косвенной оценки качества может служить сумма

сю

h= £ (Ploo.el —p[n, е]),

где р [и, е] — ступенчатая функция, соответствующая переходной функции системы; Р [со, е] — установившееся значение управляемой величины, являющаяся аналогом соответствующей интегральной оценки в теории непрерывного регулирования. Сумма 1г равна площади, заключенной между ступенчатой функцией Р [и, е] и установившемся ее значением Р [оо, е], т. е. площади отклонения ступенчатой функции Р In, г] от ее предельного значения (рис. 8.41, б).

Для косвенной оценки качества при колебательной переходной, функции используется квадратическая суммарная оценка

/*= Ё (В[оо,е] — р[л,е])2.

л=0

Методы вычисления сумм 1г и /2, не требующие решения разностных уравнений, изложены в [78].

---

8.9. Импульсные системы экстраполяции

Определение экстраполяции. Закон экстраполяции

На практике часто возникает задача выработки упрежденных значений функций, например упрежденных координат цели. Упрежденные координаты используются при наведении перехватчиков и ракет в точку их предполагаемой встречи с целью или стрельбе зенитными снарядами в точку, в которой окажется цель за время полета снаряда. Для определения упрежденных значений функции используются ее предыдущие значения. Определение значения функции в некоторой (упрежденной) точке по предыдущим значениям называется экстраполяцией, а устройства, которые решают задачу экстраполяции, называются экстраполяторами (экстраполирующими устройствами или системами).

Особенно широко экстраполяция используется при преобразовании дискретных данных в непрерывную функцию. Под преобразованием дискретных данных х [п] в непрерывные понимают создание (генерирование) непрерывной функции хэ (7) = хъ In, е], совпадающей с дискретными данными в момент их поступления (рис. 8.42). Задача преобразования дискретных данных в непрерывные возникает, например, при необходимости получения непрерывных значений координат цели по дискретным их значениям, выдаваемым радиолокатором кругового обзора. В этом случае с выхода радиолокатора на вход экстраполято-ра поступает координата цели, например, плоскостная координата х [п], в дискретные моменты времени.

Сложность задачи преобразования состоит в том, что неизвестно, по какому закону изменяется непрерывная входная функция х (7), соответствующая дискретной входной функции х [п], в промежутках между дискретными моментами времени и, следовательно, неизвестно, по какому закону следует формировать непрерывную функцию хэ [п, е] на выходе экстраполятора в этих промежутках времени. Поэтому принимают некоторый закон — закон прогноза (экстраполяции), связывающий последующие значения входной функции х (7) с ее предыдущими значениями. Благодаря этому становится возможным формировать в соответствии с принятым законом прогноза также и выходную величину экстраполятора хэ [п, е] в последующем интервале времени п t < п + 1 по предыдущим значениям.

Закон экстраполяции (прогноза). Закон прогноза зависит от тех ограничений, которые накладываются на входную функцию х (t). При определении закона прогноза изменения координат цели необходимо

т.

	Зкстраполятор

I 11 11

О 1 2п0 12

Рнс. 8.42. Преобразование дискретных данных х [п] в непрерывные (f). 266

---

X(i) A

I I

I

. 1 ! 1 > 1 1 I I I I 111 i I

i i i l li i i I

X[n]

0 12

n n+1 a

0 1 2

n n+1

Рис. 8.43. Изменение координаты x (f) цели (а) и соответствующая ей решетчатая функция х [л] на выходе РЛС (б).

учитывать ограничения на скорость, ускорение и более высокие производные движения цели. Закон прогноза определяется лишь для ограниченного участка траектории цели, соответствующего, например, периоду обзора радиолокатора.

Пусть, например, координата х (7) цели изменяется во времени по кривой АВ (рис. 8.43, а). С выхода РЛС кругового обзора эта координата выдается в дискретные моменты 7 = 0, 1, 2, п, ... с периодом, равным периоду вращения антенны (функция х [и], рис. 8.43, б). Закон прогноза изменения координаты х (t) в n-й период обзора (на. время 7 = п + е, где смещение е = At/T изменяется от 0 до 1) может быть представлен в виде полинома s-й степени относительно времени, например, частичной суммой ряда Тейлора:

x(t)=x[n, e] = *tf)j=„ +

dx(t)

dt

8 +

1 d2x (t)

2! dt*

«2 +

t+n

+

1 dsx (t)

si

dts

1 (fx (t) v! dlv

(8.89)

4=nv=0

где <Fx (f)ldtv \j=n — производная v-го порядка входной непрерывной

функции х (7) = х [n, е в момент t = п.

Из формулы (8.89) видно, что, действительно, закон прогноза учитывает значение скорости изменения входной координаты х (f), ее ускорения и более высоких производных. При определении координаты в последующий период времени 7 = п + е принимается, что эта координата продолжает изменяться с теми же значениями скорости, ускорения и т. д., какие она имела в момент времени t = п.

Очевидно, что в соответствии с законом прогноза (8.89) следует вырабатывать и координату х, [п, е] на выходе экстраполятора. Однако данные о входной координате х (7) с выхода РЛС поступают лишь в дискретные моменты времени (рис. 8.43, б) и определение производных (fx (i)/dt\ а следовательно, и использование закона прогноза (8.89) для определения хэ [и, е] невозможно. Учитывая же, что при медленном изменении х (7)

dvx(7)/d?v« Avx[n — v],

(8.90)

0 ... 85 86 87 88 89 90 91 ... 143