Раздел: Документация
0 ... 112 113 114 115 116 117 118 ... 177 □Интефал должен быть сходящимся. В случае расходящегося интеграла будет выдано сообщение об ошибке. Явно то, что интеграл, равный бесконечности, при численном ннтегрироватш узнать нельзя. Q Если точка разрыва находится посередине интервала интегрирования, то интеграл поит представить в виде суммы интегралов так, чтобы она оказалась на верхней и, соответственно, нижней границах интегрирования. При этом в полной мере проявятся достоинства модифицированного метода Ромберга. Хотя объективности ради стоит заметить, что в большинстве случаев без этой операции можно и обойтись. Однако точность при этом будет ниже. □Обычно сходящиеся интегралы от неограниченных функций можно подсчитать и с помощью адаптивного метода или (реже) простого метода Ромберга, однако точность результата при этом будет немного ниже. Пример 10.12, Численное определение несобственного интеграла от неограниченной функции Вычисление несобствен!юго интеграла с точкой разрыва ил границе интервала: Модифицированный метод Ромберга:Адаптивный метод: [ c*ln(x2)dx = -2.63580430290876[ <,"-ln(x2)dx = -2.63580430290876 Вычисление несобственного интеграла с точкой разрыва посередине интервала: •I e*.ln(x2)dx= -Ч.22900Э50150292 - 1 Очень мноше интегралы нельзя вычислить ни симьолыкии численно. Это связано с отсутствием у них первообразной н расходимостью в точке сингулярности. Поэтому при использовании численного метода будет выдано сообщение об ошибке (которое не говорит ничего конкретно), а при попытке символьного вычисления такого интеграла система возвратит первоначальное выражение. Чтобы однозначно доказать, что подобный интеграл равен бесконечности с соответствующим знаком, можно использовать метод сравнения (то есть сравнить функцию с заведомо более быстро приближающейся к асимптоте). Если интеграл функции сравнения расходится, то расходится и интеграл сравниваемой функции. Например, то, что интеграл .1 sin(x) dx ш • ."о равен -*». можно показать, используя следующий интефал сравнения: rl I . dx —> -«я 10-1п(х) 0 Вторым типом несобственных интефзлов являются интегралы с бесконечными пределами интефирования. Как и интегралы от неограниченных функций, они бывают сходящимися и расходящимися. Подсчитать сходящийся интефал можно как аналитически, гак и численно. Если же интефал расходится, в этом можно достоверно убе- литься или выполнив интегрирование символьно, илн воспользовавшись метолом сравнения. Аналитический процессор Mathcad подсчитывает несобственные интегралы с бесконечными пределами, используя теорему Ньютона-Лейбница. Кроме того, ему известны значения довольно значительного количества несобственных интегралов от функций, не имеющих первообразных в элементарных функциях. Обычно, чтобы найти значение такого интеграла, требуется применять весьма изощренные приемы, поэтому многие из них именные (Дирихле, Пуассона. Лапласа н т. д.). Нередко результатом вычисления несобственных интегралов с бесконечными пределами являются интегральные функции (например. Г-функцил Эйлера) илн их сочетания, Пример 10.13. Аналитический подсчет несобственных интегралов с неограниченными пределами Сходящиеся < простые» и именные несобственные интегралы: 1г*—II г. 4х-* - Ki 3 9 J- л 1 Г х1 . 2е я"sinfbxjdxassume.a >0 е dx-* n J "-------- 2 и2 а + b Случай полной неопределенности: Г sin(x) dx -* undefined О Пример интеграла, результат для которого выражается через символьные функции: Г - х I е х dx assume ,1 > О -* T(t)-t О Если аналитически найти значение несобствен нога интеграла с бесконечными пределами не получается, расчет следует провести численно, Для этого в Mathcad имеется специальный метод Infinite Limit (Бесконечный предел). Самостоятельно выбирать данный метод вам не придется, поскольку система автоматически переключается на него при введении в оператор интегрировании символа бесконечности. Точность данного алгоритма весьма значительно зависит от значения TQL. Пример 10.14. Вычисление интегрела с бесконечным пределом Точное аналитическое решение: Г - х1 е sin(x)dx -> - = 0.5 О2- Обычная точность (TOL-JfT*):TOLIir": еГ *sin(x)dx - 0.499999999986754е~ **in(x) dx- 0.5 Использование для вычисления интегралов с бесконечными пределами обычных методов (Ромберга или адаптивного) либо (ь лучшем случае) приведет к сообщению об ошибке, либо (в худшем случае) будет выдан неверный результат. Имеется ряд ограничений на применение численного интегрирования для определения нессюствснных интегралов с неограниченными пределами. Так, использовать его для нахождения расходящегося интеграла не стоит в любом случае. Также не получится произвести расчет, если интефал сходится неравномерно. Это прежде всего относится к периодическим функциям, например вида f(>)=sin(x)/x. Впрочем, многие несобственные интегралы от такого рода функций uoryi быть подсчитаны символьно. Чтобы подсчитать кратный интеграл, выполните следующую последовательность действий. 1.Введите командой панели Calculus (Вычисления) или еоответствукицим сочетанием клавиш нужный оператор интегрирования. 2.Поставьте курсор в маркер надытгтегральноЙ функции и введите второй оператор. Для вычисления тройного интефала повторите эту операцию два раза. 3.В маркере последнего из заданных операторов пропишите интефируемую функ- 4 Заполните маркеры лнффгчмпистпптм порядке, в котором должно вестись нн-тефирование. 5. Если вычисляется определенный интеграл, заполните соответственно маркеры пределов интефмривания. Все те выводы и рассуждения, которые были сделаны нами относительно символьного и численного определения интеграла от функции одной переменной, в полной мере могут быть перснесены-и на случай кратного итерирования. Эта возможность объясняется тем, что для вычисления интегралов обоих типов используются одни и те же алгоритмы. Пример 10.15. Символьное и численное вычисление кратного интеграла 10.5. Вычисление кратных интегралов цию. Г 1-х -.ydydx->-I2b + 6-Ь * 12а -б-а 1-7х 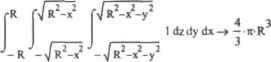 Очень внимательно при задании кратного интефала следует относиться к последовательности определения пределов интефнпования. Неправильно согласовав их с перс- 0 ... 112 113 114 115 116 117 118 ... 177 |












