Раздел: Документация

0 ... 110 111 112 113 114 115 116 ... 177

дабы получить максимально точный результат, При этом интегрирование почти наверняка не будет успешным. Обычно минимальное значение T0L дляметода Ромберга лежит в пределах от 10"* до Ю-",

□ Очевидно, что алгоритм Ромберга не предназначен для интегрирования функций с разрывами. Причем это касается как разрывов 2-го рода (в случае которых численное интегрирование в принципе возможно лишь, если первообразная в соответствующих точках непрерывна или имеет разрыв первого рода), так и разрывов 1-го рода, при наличии которых, казалось бы, подсчет интеграла не должен представлять особой сложности. Чтобы проинтегрировать функцию с разрывами первого рода, используйте адаптивный алгоритм (если для этого применить метод Ромберга, то ответ будет получен с большой погрешностью или же алгоритм попросту не сойдется), Об особенностях интегрирования при наличии точек разрыва 2-го рода мы поговорим в следующем разделе.

Численные методы интегрирования схожи в основных своих идеях. Поэтому те выводы, которые мы сделали на основании анализа метода Ромберга, можно автоматически перенести и на остальные реализовали we в Mathcad методы. Особенно важно запомнить сведения о ключевой роли системной константы ТОЬдля получения точного результата. 11а примере продемонстрируем как. уменьшая TOL, можно добиться нужной точности ответа.

Пример 10.9. Влияние T0L на точность численного интегрирования

Точность численного интегрирования мы будем оценивать, сравнивая результаты, полученные численными методами, с точным аналитическим решением;

г 100л

standard

sui(x) I 599 dx - +--n

I + cos(x)

-

6

11 оследоиател lно уменьшая величину TOL, посмотрим, как это будет влиять па точность результата

-10Ои

TOL:= 10

TOL 10

«<я[хГ 1 + сга(х)

d*-«indard =4X021318500079929

ft

rlDOn

—-d*-»landini = -4.9283437*199447 * 10 7

1 coi(x)

TOL:- 10

12

HHJn

»(x)

1 + cos(k)

d* - rtandanl =3.82556208933238*10

Если уменьшить TO Lao 10". алгоритм не сойдется (рис. 10.4). Следовательно, полученный при "1 и [.- Ю " ответ является максимальна точным й случае использования метода Ромберга.

---

10.3. Численное вычисление определенного интеграла * 353

.-13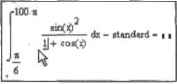

TOL >• 10

1 Canl саггуеаэа to а зоМоп

Рис. 10.4. Если TOL присвоено слишком малое значение, то численный алгоритм не сойдется

□ Adaptive (Адаптивный). Метод, предназначенный для вычисления интегралов от функций, быстро изменяющихся па промежутке. Главная идея, лежащая в его основе, заключается в том, что ширина интервала разбиения не постоянна, как в случае метода Ромберга, а изменяется в зависимости от скорости изменения функции. В большинстве случаев данный алгоритм дает более точный результат, чем метод Ромберга (поэтому он используется Mathead по умолчанию). Впрочем, как правило, различия между ответами этих численных алгоритмов начинаются после 9-10-го знака, поэтому нет принципиальной разницы, какой из них использовать при решении обычных практических задач. Впрочем, одно существенное преимущество у адаптивного метода есть. С его использованием можно интегрировать функции с разрывами первого рода (метод Ромберга в таких случаях дает большую погрешность или не сходится), а также с разрывами второго рода при условии, что первообразная в соответствующих точках непрерывна (или имеет разрыв первого рода).

Пример 10.10. Численное интегрирование с использованием адаптивного метода

При использовании адаптивного метода результат обычно получается немного точнее, чем при применении метода Ромберга:

I "

standart :=

dx-> —ln(3)+ - + ln(2) 233

Адаптивный метод:

1п(х2)

dx- standan = О

Метод Ромберга:

1п\х2),-М

dx - standart = -2.803 х [Q

Адаптивный метод дает гораздо лучший результат, чем метол Ромберга, если на промежутке интегрирования имеются точки разрыва первого рода. Например:

Адаптивный метод:Метод Ромберга:

rlOO

Ля

dx=200

100

+ Adx= 199,941

---

Адаптивный метод, в отличие от метода Ромберга, может быть использован для интегрирования фукюптй с разрывами второго рода (прн непрерывности первообразной в точках разрывов):

□Infinite Limit (Бесконечный предел) Этот метод используется для подсчета несобственных интегралов с неограниченными пределами. Подробно его мы разберем в следующем разделе.

□Singular Endpoint (Сингулярный предел). Данный метод применяется для определения несобственных интегралов от неограниченных функций, если точка разрыва совпадает с границей интегрирования.

Обычно численный подсчет интеграла не вызывает особых сложностей. Но что делать, если Mathcad не сможет решить задачу? Во-первых, проверьте правильность задания интегрируемой функции и пределов интегрирования Во-вторых, попробуйте сменить численный метод. Иногда адаптивный метод справляется с интегрированием таких функций, перед которыми пасует метод Ромберга. В-третьих, увеличьте значение TOL Если установленный уровень точности слишком высок, то численный алгоритм может просто не успевать сходиться в рамках отведенного на количество итераций лимита. В-четвертых, проанализируйте поведение функции на интервале интегрирования с помощью графика. Вполне возможно, что она имеет точки разрыва второго рода. Об особенностях интегрирования таких функций мы поговорим в следующем разделе.

В классическом математическом анализе при введении понятия определенного интеграла обычно предполагается, что интегрируемая функция ограничена, а интервал интегрирования конечен. Однако оказывается, что при соблюдении ряда условий опре-делсипый интеграл может иметь смысл и в случае функций, имеющих разрывы второго рола (то есть бесконечно возрастающих по абсолютному значению при приближении к некоторой точке), а также прн бесконечных пределах интегрирования. Подобные интегралы называются несобственными, и в их вычислении имеется масса особенностей по сравнению с обыкновенными (собственными) интегралами. Есть два типа несобственных интегралов: от неограниченных функций и с бесконечными пределами. Вычисляются они совершенно по-разному, поэтому стоит рассмотреть их по отдельности. Начнем мы с интегралов от неограниченных функций. Рассмотрим функцию f(x). имеющую разрыв второго рода в точке х-Ь. Возможно ли, и если да, то при каких условиях, найти определенный интеграл в интервале от некоторой точки х-а до точки разрыва? Оказывается, что это реально, если первообразная для f(x) в области точки разрыва конечна (но не обязательно непрерывна). При этом соответствующий интеграл будет называться сходящимся, и по смыслу он будет совпадать с обычным определенным интегралом. Если же первообразная будет иметь в точке Ь разрыв второго рода, то несобственный интеграл будет называться расходящимся и равняться бесконечности. Также важным условием для того, чтобы можно было най-

-dx-6.78

10.4. Особенности вычисления несобственных интегралов

0 ... 110 111 112 113 114 115 116 ... 177