Раздел: Документация
0 ... 113 114 115 116 117 118 119 ... 177 менпыми под знаками дифференциалов, вы получите неверный ответ. Ошибка такого рода — самая распространенная при вычислении кратных интегралов. При вычислении кратных итггегралов осторожно нужно относиться к использованию численных методов. Связано это с тем, что если кратность интеграла равна трем или более и интервалы интегрирования относительно широкие, то количество шагов численного алгоритма, которые требуются для получения более или менее точного значения, просто огромно. А это означает, что время расчета такого интеграла численным методом будет весьма заметным даже на мощном современном компьютере. Так, посмотрим, сколько времени в секундах может понадобиться для вычисления чпроблем-ного» тройною интеграла: timeO <- timefO)= 349.863 г 100 (-200 rlOOO INT ч- Jатп(х+ у + z) dxdy dz - 100 - 200 - 1000 time(l) - timeO Изданного примера следует вывод: численные методы примешпъ тогда и только тогда, когда с поставленной задачей не справится символьный процессор. 10.6. Численные методы интегрирования Численное интегрирование - пожалуй, одна из самых важных задач прикладной математики. Методов ее решения было создано великое множество, и каждый из них имеет свои достоинства и недостатки. Естественно, описывать их все в рамках данной книги нет никакого смысла поэтому мы остановимся лишь иа некоторых основополагающих идеях, а также опишем один из методов, использующихся системой Mathcad. Так как, н отличие от численного решения уравнений, успех интегрирования не так сильно зависит от вашего знания идей используемого метода, то читать данный раздел совсем не обязательно, если в своей практике вы не сталкиваетесь с необходимостью самостоятельно создавать численные алгоритмы. Однако это будет полезно как с точки зрения кругозора, так и какоченьненлохая тренировка техники программировании в Mathcad. Тем более численные методы интегрирования входят в курс математики технических и естественных специальностей вузов, поэтому в самостоятельной* реализации численного метода может заключаться домашнее задание. Суть любого численного метода интегрирования состоит в приближении функции другой кривой, площадь пол которой можно более или менее легко подсчитать аналитически. Обычно в качестве таких кривых используктгея кривые алгебраических полиномов. Самым ранним исторически и наиболее известным численным методом ннтефирова-ния является метод средних прямоугольников. Идея его вытекает из самого определения интеграла как предела суммы произведений ширины интервала разбиения назначение функции в его середине. То есть гладкая криволинейная трапеция заменяется на ступенчатую фигуру, площадь которой приближается к площади трапеции при стремлении ширины интервала разбиения к нулю. Иллюстрация метола средних прямоугольников показана иа рис. 10.5, а. 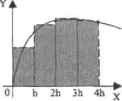 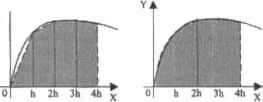 а6в Рис. 10.5. Иллюстрация основных методов численного интегрирования Совсем не трудно вывести общую формулу данного метода: =1 i = l Здесь п - количество разбиений интервала интегрирования, h - ширина среднего прямоугольника. Лля того же, чтобы реализовать в системе Mathcad такой простой алгоритм, которым является метод средних прямоугольников, даже не придется прибегать к использованию языка программирования; РпХа.Ь.п) :« i 1 Ь-а Проверим, правильна ли работает заданная функция: гтдТ.а.Ь.п):- —— а + ——М ~ з J i => 1 ftinc(x) sbl к) \ func(x) dx float, 10 -+ .265488009 func, 0,-, 1000 V3 J 0.2654879007 Проверка показывает, что прн больших п метод средних прямоугольников может быть весьма точен. Так, в рассмотренном примере 1000 разбиений дали результат, верный до пяти знаков. Для большинства практических задач это более нежели достаточная точность. А вычислить функцию 1000 раз и просуммировать полученные значения — лто для современного компьютера дело, требующее долей секунды. Поэтому можно было бы остановиться на методе средних прямоугольников как на вполне приемлемом для подсчета интегралов на небольшом интервале. Однако если с помощью рассматриваемого алгоритма понадобилось бы вычислить с той же точностью тройной интеграл, то количество разбиений возросло бы до 10 000 000. А подсчитать столь КС раз значение сложной функции - это уже дело нескольких часов (а лет 20 назад это была бы вообще малоразрешимая задача). Приведенные цифры иллюстрируют очевидную необходимость найти какойто другой метод численного интегрирования, ко- торый,прн сохранении точности, требовал бы меньшего количества узловых злачгний функции. Уменьшить количество разбиений можно прежде всего, увеличивая точность приближения функции легко интегрируемой аналитически кривой. Наиболее простая из таких кривых — это прямая. Метод, основанный на приближении фрагаентов кривой функции секущими, проходящими через границы интервалов разбиения, называется методом трапеций (см. рис. 10.5,6). Точность данного метода близка к точности метода средних прямоугольников, и величина ошибки пропорциональна квадрату ширины шгтервала разбиения. Общая формула метода тралений будет вполне очевидна, если вспомнить, каким образом в геометрии вычисляется площадь этой фигуры: •=1 i - 1 -[fi>+ hi) + rTa + h-fl -1)]] Задать в Mathcad функцию, вычисляющую интеграл по методу трапеций, столь же просто, как и в случае метода средних прямоугольников: Int(f.a.b,o):- £ /Ь-а *\ ГЬ-а ч Ч--.+ »\ + i--U-U + i func(x) := sin(x) X г V, ftuic(x)dx float, 10 -► .265488009 Intftn>c,0,j,1( 2654882245 Точность результата вычисления интеграла по методу трапеций, полностью в соответствии с теоретическими выводами, оказалась крайне близкой к точности метода средних прямоугольников. Соответственно точность данного метода нас вряд ли может удовлетворить. Невысокая точность метода трапеции легко объясняется тем, что все-таки приближение кривой функции ломаной из отрезков секущих является довольно грубым даже для значительного количества разбиений. Чтобы уменьшить ошибку интерполяции, попробуем использовать для приближения функции полином второй степени — параболу. Идея вычисления интеграла с помощью парабол довольно проста: промежуток разбивается на неширокие интервалы И на каждом ИЗ НИК вычисляется площадь, ограниченная интерполирующей функцию параболой (см. рис. 10.5, в). Чтобы задать приближающую параболу, нужно знать коэффициенты ее уравнения. Конечно, можно просто разложить в средней точке интервала функцию в ряд Тейлора — но это, пожалуй, слишком сложно и не очень надежно. Гораздо проще можно справиться с данной задачей, использовав возможности Mathcad но решению систем уравнений. Так как уравнение параболы имеет три коэффициента, то. исходя из известного правила алгебры, чтобы их найти, нужно задать систему соответственно из трех уравнений. Сделать это можно, 0 ... 113 114 115 116 117 118 119 ... 177 |












