Раздел: Документация

0 ... 116 117 118 119 120 121 122 ... 177

Вычислив приближения по Сим пеону, можно получить приближения еще на два порядка более точные, если применить рекуррентную формулу Буля:

16S(f,b)-S(f,2b? 15

В общем виде формула уточнения имеет вид:

щ. k?=4kR(J,k-l>-R(j-l,k-l) 4k-l

Проще всего понять ее смысл можно, представив себе соответствующую таблицу приближений. Первый столбец на j элементов будет полностью заполнен приближениями, полученными с помощью рекурренп юЙ формулы трапеций. Приближений по Симлсону будет на одно меньше, поскольку первое приближение алгоритма трапеций не имеет верхней, вычислепной при вдвое большем шаге, пары. Соответствен но в столбце приближений, вычисленных по формуле Буля, не будет двух верхних элементов, в следующем столбце — трех и т. д. В результате будет получена нижняя треугольная матрица, элемент нижнего правого угла которой и является наиболее точным приближением (рис. 10.6).

RCJ.0)

Формула [трапеций

ад и

Формула Снмпсона

ЩИ) Формула Буля

Щ 3)

Третье приближение

Четвертое приближение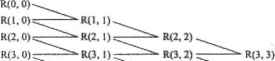

0 1

: з

R(4,0} щ4, 1). "" щ4, 2) К(4,3)К(4, 4)

Рис. 10.в. Схема интегрирования по Ромбергу для пяти приближений

Если отнять полученную при вычислении интефала по Ромбергу матрицу от соразмерной, все ненулевые элементы которой - истинные значения подсчитываемого интеграла, поделить на величину истинного значения и умножить на 100, то в результате получится характеристическая мафица процентных ошибок приблизительно следующего вида:

( 38.7894ОО

21.46018 -4.71976О

5.19406 -0227990.07146

0 О

(1

o

о

о

1.28842

-0.01346 8.4345510 * -2.775x10 4

0.32148 -82955x10 4 1.2375x10 5 -8.15х 10 7 2.7 х 10 7 0

к, 0.08033 -5.167х Ю

,-5

1.9 х 10

„- 7

~5х 10

---

Из этой матрицы видно, сколь быстро убывают ошибки последовательных приближений, вычисляемых с помощью описанных рекуррентных формул. Самих же вычислений при этом нужно сделать очень немного. Поэтому метод Ромберга нетолько очень точен, но и весьма быстр.

4. В программной реализации алгоритма Ромберга удобно осуществлять одновременное нахождение всех возможных для данного шага приближений (то есть на каждом круге никла white заполняется одна строка приведенной выше матрицы, начиная со второй):

for ke 1..J

4Ч,к-Г Vt.k-l 4k-1

В качестве условия остановки цикла в методе Ромберга обычно используют критерий разности двух последних приближений, лежащих на диагонали матрицы (R, ( и Rj.jj)- В том случае, если разность по модулю окажется MeitbiueTOL, то цикл будет остановлен и в виде ответа будет выдано последнее приближение:

break ii-R

<TOL

Как видите, реализация метода Ромберга, в общем, несложна. Однако все равно стоит привести соответствующую программу в «собранном» виде:

Roraberg(fta,b,TOL) :=

ь - а)

0 г

while 1 J <- J+ 1

J

(fi» + Щ)

2

p=l

for Ice 1..J

4ltRJ,k-l"RJ-].k-]

4k-l

break If IRj-R

<TOL

---

Проверим, насколько качественно работает написанная программа. Для этого сравним результат расчета интеграла, произведен но го ею, с точным аналитическим значением данного интеграла:

Как видно из приведенных примеров, эффективность написанной программы очень высока и точность результатазначительно превышает точность уровня T0L Кроме того, алгоритм очень быстро сходится и расчет даже с предельной точностью занимает долг секунды. А это означает, что метод Ромберга можно применять для вычисления интегралов любого типа, а также кратных интегралов.

Описывать остальные встроенные в Mathcad методы мы не будем, прежде всего по причине ИХ специфичности. При желании информацию о них вы сможете найти в справочной системе программы или в книге, посвященной численным методам.

0 ... 116 117 118 119 120 121 122 ... 177