Раздел: Документация
0 ... 114 115 116 117 118 119 120 ... 177 вычислив значение приближаемой функции в трех точках интервала. Наиболее просто выбрать в качестве таковых границы н середину интервала разбиения. В результате получим следующую систему уравнений: А-хО2 + В-х0+С=ГО А(хО+ h) + В-(хО+ h) +• С= П A-(x0+ 2h)2 + В-(хО+ 2-h) + С= f2 Здесь хО — левая граница интервала; h — шаг, соответствуюншй расстоянию между узловыми точками; fO,fl, f2 — значения функции на левой границе, в середине, на правой границе интервала; А, В, С — коэффициенты уравнения параболы. Система является линейной относительно коэффициентов, поэтому у нее будет только одно решение. Это означает, что через три точки можно провести одну единственную параболу (справедливо и обобщение — через п точек проходит только один полином степени п-1). Решить заданную систему очень просто илн посредством оператора solve, или матричным способом. Ввиду объемности выражений для коэффициентов, создадим переменные А. В и С, которые будут на них ссылаться: COF:= Ах В-хО+ С= ТО А(хО+ й) + В{хО+ Ь) + С= П solve. А, В, С А-(хО+ 2-h} + В-(хО+ 2-Ы + С= f2j А := (COF7В := (cof\С > (fOr7), После того как коэффициенты приближающей параболы будут определены, элементарно можно найти площадь, которую ограничивает ее фрагмент на интервале интегрирования: гхО+2-h 2 А-х + В-х+ Cdx simplify I ИГО + ФП + tl) Полученная общая формула называется формулой Симпсона, и с ее помошью можно находить значение интеграла, и не решая систему уравнений для каждого интервала разбиения. Достаточно вычислить три узловых значения интегрируемой функции. Реализация метода Симпсона в Mathcad будет выглядеть следующим образом: Simrtf.a.b.nl :=~ I = I b -а Зп 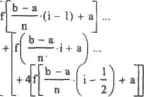 func(x) := Binfjgx Cuocfx} da float, 15 -» ,26548800861814 Simn ftinc. 0, у, tooj » 0.265488008580604 При количестве разбиений, в 10 раз меньшем, чем было использовано для расчета интеграла методами средних прямоугольников и трапеций, точность результата оказалась на 5 (I) порядков выше. Л это означает, что метод Симпсона можно уже использовать и для вычислений кратных интегралов. Приближать интегрируемую функцию можно полиномами и более высокой степени Обычно для этого используются полиномы 3-й и 4-й степени (описываются соответственно формулой Симпсона 3/8 и формулой Буля). Получить формулы для них можно точно так же, как мы поту шли формулу Симпсона. В общем случае, чем выше степень интерполирующего полинома, тем точнее приближение. Так, ошибка при вычислении интеграла по формуле Буля убывает пропорционально 6-й степени величины интервала разбиений (формула Симпсона на два порядка менее точная). Из-за ряда технических сложностей полиномы выше 4-й степени используются редко. Чтобы более объективно сравнить эффективность работы рассмотренных методов, определим подбором то количество разбиений, которое требуется для каждого из них, чтобы приблизить интеграл с заведомо известным аналитическим решением с точностью до 10-го знака мантиссы; г* x)ain(x)I Дх)ак- Г Pr(f.0.x, lOOOOO)- 2 8.2235551701614895x10" 11 UA (f,0,rt,IJOOOO)-2»-9.7301278145778269*10" " Simp (f,0,R,170)- 2 = 8.099к JO- 11 Полученные цифры не могут не впечатлять: при использовании метода параболы разбиений требуется почти в 1000 раз меньше, чем доя методов средних прямоугольников и трапеций. Для достижения же стандартной точности (0,001) будет достаточным разбить промежуток всего на 4 (I) интервала; Simp (f.0.a,4) = 2 00026917 Благодаря такой высокой эффективности формулы Симпсона до появления компьютерной тех»гики ее использовали для подсчета интегралов, которые нельзя было вычислить аналитически, на бумаге. Кстати, если использовать, например, формулу Буля, то разбиений потребуется еще меньше. В теории численных методов имеются формулы, используя которые можно предсказать, какой будет порядок у ошибки при вычислении интеграла от функции 1(х) на промежутке от а до b с шагом h. Соответствующая формула для метода трапеций имеет вид: o(h2)= (о - а) dx h2 Формула для ошибки метода Симнсона будет схожей: (Ь - а) А J 180 Данные формулы показывают, что ошибка зависит прежде всего от величины шага. Также на нее будет влиять ширина интервала интегрирования (чем больше шагов Придется проделать алгоритму, тем сильнее будут сказываться накапливающиеся погрешности) и скорость изменения функции (чем она выше, тем больше будет погрешность). Количественно скорость изменения функции можно узнать, вычислив производную. Однако производная даст мгновенную скорость, а нам нужно знать среднюю скорость изменения функции на промежутке интегрирования. Поэтому необходимо найти среднее значение производной на промежутке. Именно эти величина фигурирует в приведенных выше формулах. Формулы ошибки методов численного интегрирования важны в связи с тем, что они позволяют определить, насколько малым должен быть шаг, чтобы была достигнута необходимая точность. Например, попробуем узнать, какой величины нужно сделать шаг, чтобы вычислить интеграл от f(s)=sm(x) на промежутке от 0 до я методом Симнсона с точностью до 5-го знака. Выразив из формулы ошибки метода Симнсона h, получим следующее неравенство: li S 180TOL (b-a)-f(x) dx Все входящие в данное выражение величины, кроме среднего значения производной, нам известны. Чтобы найти недостающую величину, рассчитаем четвертую производную аналитически, после Чего найдем среднее значение полученной функции на промежутке, используя следующее замечательное свойство интеграла: f[x) Ь - a J ffxjdx Расчет: —jsiofx) -> sin(x) dx I n J sin(x)dx-> — Зная среднее значение производной на промежутке, находим ветчину шага и количество шагов: —jSin(x) -» sin(x) dx 1 Г • — • sin It Jn (x)dx -+ — n 0 ... 114 115 116 117 118 119 120 ... 177 |












