Раздел: Документация

0 ... 109 110 111 112 113 114 115 ... 177

Так как участки кривой симметричны относительно точки разрыва в х=0, но противоположны по знаку, то, очевидно, данный интеграл должен быть равен 0. Этот результат будет получен при проведении интегрирования численно:

— dx=0

Однако при аналитическом интегрировании результатом будет довольно странное комплексное значение:I

г1

I9 3 2

— dx ->----ir3

Зг 4 4

1

Чтобы понять, в чем кроется причина ошибки программы, найдем первообразную для интегрируемой функции, а затем построим ее график (рис. 10.3).

1 а 33

— dx-* --х

3

а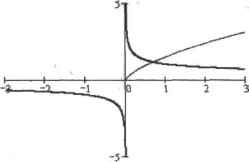

Рис, 10.3. Интегрируемая функция определена на всей числовой оси. кроме точки х=0. Ее первообразная существует пишь при неотрицательных значениях аргумента

Итак, использовать теорему Ньютона-Лейбница в случае рассматриваемого интеграла нельзя, так как первообразная не определена в действительной области при х—1. Mathcad же этого, судя по всему, не учгггывает.

3 з

1

F(l) - P(-l) srnipUfy - - - i-32

---

Как избежать ошибок, подобных описанной? Во-первых, строить график интегрируемой функции и, по возможности, ее первообразной. Во-вторых, сопоставлять результаты аналитического и численного интегрирования. В-третьих, главное, не полагаться полностью на программу и относиться осторожно к полученным результатам. И помните, что невозможно эффективно использовать Mathcad, посредственно владея математикой. Найти н исправить ошибки при этом просто нереально.

10.3. Численное вычисление определенного интеграла

В том случае, если системе не удается найти первообразную функции, приходится использовать методы численного интегрирования. Численное интегрирование в Mathcad - .что куда более тонкая операция, чем интегрирование аналитическое. Зачастую, чтобы получить правильный ответ, нужно верно задать точность, выбрать наиболее эффективный алгоритм, проанализировать поведение функции и, при наличии точек разрыва, представить интеграл в виде суммы интегралов... Неплохо также иметь общие представления об алгоритмах численного интегрирования, чтобы понимать. В каких случаях они могут быть использованы, а в каких нет. Этот раздел посвящен рассмотрению важнейших принципов численного интегрирования в Mathcad.

Если вы хотите использовать численный метод, прежде всего присвойте всем параметрам, входящим в интегрируемую функцию, конкретные значения. Пределы интегрирования, естественно, также должны быть числами. В качестве оператора вывода следует использовать оператор численного вывода <s-»,

Пример 10.8. Численный расчет неберущихся интегралов

Зя

Г

1--dx = 4.

-1

sin 1X1

dx= 1.608

/-L0

x

— dx= 2.501x Iff x

В систему Mathcad разработчиками было встроено несколько численных методов интегрирования. Необходимость этого связана с тем, что алгоритмы численного интегрирования не столь универсальны, как алгоритм дифференцирования. Каждый из них подходит для определенной группы функций или тина интеграла. Так, например, такие классические методы, как метод трапеций, средних прямоугольников или Симп-сона, хороши лишь в случае гладких непрерывных функций и небольшого интервала интефирования. Для того же, чтобы подсчитать интеграл с бесконечным пределом или интеграл от функции, имеющей точку разрыва второго рода на границе промежутка, нужно использовать принципиально другие подходы, отличающиеся от банального разбиения на равные элементарные отрезки.

eK-ln(x)dx=-1.3I8

о

---

10.3. Численное вычисление определенного интеграла «351

Чтобы произвести смену численного метода, щелкните правой кнопкой мыши на операторе интегрирования. При этом откроется его контекстное меню, содержащее список вариантов возможных алгоритмов интегрироваиня.

□AutoSetect (Автоматический выбор). Метод интегрирования выбирается системой автоматически. Лучше всего, если по умолчанию у вас будет отмечен именно этот пункт. В большинстве Случаев этого вполне достаточно для того, чтобы интеграл был подсчитан максимально правильно и без вашего участия. Однако опыт показывает, что в некоторых ситуациях (прежде всего при наличии точек разрыва), система может не справляться с правильным выбором численного метода (Это Связано с тем, что, как правило, автоматически Mathcad выбирает либо адаптивный метод (Adaptive), либо метод бесконечного предела (Infinite Limit)). Если вы столкнулисье проблемой при вычислении итггеграла, попробуйте сменить алгоритм подсчета. Для этого вам нужно сделать правильный выбор из следующих четырех методов.

□Romberg (Ромберга). Весьма эффективный метод, применяемый для вычислении интегралов от функций, не имеющих особенностей (разрывов первого н второго рода, областей резкого изменения). Является основным в Mathcad. Упрощенно его можно описать следующими шагами:

1)в качестве самого первого приближения вычисляется значение площади трапеции, основания которой проведены через границы промежутка интегрирования.

2)затем запускается цикл. На каждом его круге шаг уменьшается вдвое, На первом обороте цикла вычисляется приближение по формуле трапеций из того условия, что интервалов интегрирования уже 2. На втором круге шаг будет уменьшен в четыре раза относительно первоначального, и соответственно трапеций также будет просуммировано четыре. И так далее до тех пор, пока не будет выполнено условие остановки цикла;

3)в качестве условия остановки цикла в методе Ромберга обычно используют критерий разности двух последних приближений. В том случае, если разность по модулю окажется меньше T0L, то цикл будет остановлен и в качестве ответа будет выдано последнее приближение.

Данное выше описание метода Ромберга является предельно упрощенным. Реально же данный метод заснет использования ускоряющих сходимость и увеличивающих точность математических приемов, куда более стожен (обстоятельно его мы разберем в разд. 10.6). Но несколько важных выводов можно сделать даже из такого примитивного описания.

□Точность результата численного интегрирования всегда выше или равна ТОL Поэтому, если нужно получить ответ, правильный до пятого знака мантиссы, T0L нужно присвоить значение 10

□Чем выше TOL, тем больше оборотов должен будет проделать цикл алгоритма. Следовательно, время расчета резко возрастает с увеличением T0L Это может быть существенно в случае кратных интегралов или при интегрирований функции на широком интервале

□В любых численных расчетах на компьютере имеется погрешность, у которой есть свойство накапливаться. Если расчет интеграла потребует слишком большого количества итерапий, то погрешность может значительно превысить уровень желаемой точности. Чтобы этого не произошло, в реализацию метода Ромберга Mathcad введено ограничение на количество итераций. Если оно будет превышено, то система возвратит сообщение об ошибке: Cant converge to a solution (Не сходится к решению). Это означает, что не стоит стремиться присвоить TOL минимальное значение,

0 ... 109 110 111 112 113 114 115 ... 177