Раздел: Документация

0 ... 133 134 135 136 137 138 139 ... 177

13.3.1. Экстремум функции одной переменной

Поиск экстремума функции — это задача, технически очень схожая с поиском корней уравнения. Критерием существования корня в некоторой точке является то, что величина функции в ней по модулю должна быть меньше некоторого, определенного в системе кли пользователем, параметра точности. При поиске же экстремума меньше этого параметра должна быть не сама функция, а се первая производная. Минимум же это или максимум, можно определить по знаку второй производной.

В программе Mathcad существуют две функции, отвечающие за поиск экстремумов: Minimiie(f,xi,)c2...,) (определяет локальные минимумы) и Maximize (ьх1д2....) (ищет локальные максимумы). Синтаксис их довольно схож с синтаксисом функций решения уравнений (root, find) и имеет два возможных варианта заннс и Единственным отличием в синтаксисе функций Maximize. Minimize н root является то, что при поиске экстремумов в скобках соответствующей встроенной функции должно быть заключено л ишь имя исследуемой функции, без переменных, от которых она зависит. Если вам известно приблизительное расположение нужной вам точки экстремума, то можно воспользоваться более простым стандартным вариантом употребления функций Minimize и Maximize. В этом случае требуется задать начальное приближение.

Пример 13.3. Поиск экстремумов с помощью функций Minimize и Maximize при заданном начальном приближении

в;х)>х3-Зх-1 х:>1

Maximize(f.x) * -I MmLmize(f,х) 1

Убедиться в правильности полученных результатов можно, построив график.

Если вы щелкнете правой кнопкой мышн на тексте функции Minimize или МаИгтм, то откроется контекстное меню, практически полностью аналогичное меню функции find. Отличие в них есть только одно: поиск экстремумов нельзя произвести с помощью метода Левенберга. Так что, если функция не справится эффективно со своей задачей, вы можете поменять используемый метод илн самостоятельно произвести его настройку.

13.3. Численное определение экстремумов функций

Очень многие математические задачи решаются с помощью определения точки экстремума соответствующей функции, Учитывая важность данной проблемы, разработчики Mathcad внесли и программу специальные функции, которые, используя возможности численных алгоритмов решения уравнений, могут весьма эффективно с ней справляться. Однако использование градиентных методов {а именнотакие алгоритмы лежат в основе поиска экстремумов функций) сопровождается многочисленными сложностями, связанными с правильным выбором начальных приближений, точности настроек метода. Поэтому в этом разделе мы попробуем разобраться, как можно быстра и просто найти точки минимума или максимума с помощью системы Mathcad и как при этом не допустить ошибок.

---

Впрочем, как показывает опыт, это вряд ли поможет (ввиду того, что эффективность как квазинютоновского метода, так и метода сопряженных градиентов практически совпадает).

Эффективность работы функций Minimize и Maximize сильно зависит от выбора точки начального приближения. Особенно это проявляется в тех случаях, когда количество локальных минимумов или максимумов велико.

Пример 13.4. Исследуем функцию (рис. 13.5)

X(t) :=2е~ l-coB(6t)

1~1

.2j.

I

i

Рис. 13.5. График функции, описывающей затухающие колебания

Функции, подобные этой, в теоретической механике применяются для описания затухающих колебаний. Поэтому график отображен только начиная с 0, поскольку время не может быть отрицательной величиной.

Экстремумов, равно как и корней, данная функция имеет бесконечное множество, Посмотрим, какой результат дадут функции Maximize и Minimize при различных приближениях;

1:=0

Maximizc(X,0 = -0.028 Mmirruzc(X,l) =0.496

Отрицательная координата максимума была получена потому, что, чисто с математической точки зрения, данная функция существует и в отрицательной области, причем там она совершает колебании с увеличивающейся амплитудой но направлению к бес* конечности.

I :=10

rvfaximize(X,t) = 2.067 Minimize(X,t) - 2.59

Интересно, что су шествуют локальные экстремумы, которые расположены ближе кЮ, чем полученные с помощью функций Maximize и Minimize. То, что они не были обнаружены, связано, скорее всего, с их малой амплитудой.

Г.10000

Maximize(X,t) = 1x10 Minimize(X.l) = 1 х 10

---

На этот раз действительно получился странный результат: если верить Mathcad, данная функция имеет в одной точке одновременно и минимум, и максимум! Естественно, реально такого быть никогда не может. Попробуем объяснить причину допущенной ошибки.

Как вы помните, главным условием существования в точке экстремума является условие равенства производной пулю. Рассматриваемая функция является убывающей, и при значении переменной 10 ООО с точностью, значительно превышающей границу нуля в Mathcad, равняется нулю. Производная же по величине в данном случае должна быть близка к функции. Таким образом, получается, что для всех точек, начиная с некоторого значения tB, будет выполняться условие экстремума. Тип же экстремума определяется обычно по знаку второй производной, которая в данной ситуации также должна бесконечно близко приближаться по значению к нулю. Из-за этого возникает неопределенность, и обе функции относят данную точку к экстремуму своего типа.

И, наконец, если мы попробуем ввести большое по модулю приближение из отрицательной области, то никаких значений экстремумов найдено не будет. Причина же этого довольно очевидна: при таких значениях l функция принимает стишком большие по модулю значения.

Делая вывод, можно сказать, что правильный ныбор Начальной Гички играет принципиальную роль при поиске экстремумов. А осложнить выполнение этой работы могут те же особенности поведения исследуемой функции, что и при решении уравнений: множественность экстремумов, разрывы, особенности поведения функции на бесконечности. Поэтому к полученному результату нужно относиться очень внимательно и стараться всегда проверять его верность с помощью графика. Благо, в случае функции одной переменной это можно сделать очень легка

Второй возможной формой употребления функций Minimize и Maximize является запись их в составе вычислительного блока, подобно функции find. При такой форме стгтак-енса появляются некоторые допешттельные возможности. Например, записав ниже ключевого слова Given систему неравенств, вы сможете произвести поиск экстремумов на определенном интервале изменения переменной. Также здесь вы сможете ввести некоторые ограничения иа значения минимума или максимума.

Пример 13.5. Рассмотрим функцию (рис. 13.6)

в» :* -х7 + 4х3 - Зх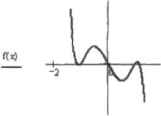

0 ... 133 134 135 136 137 138 139 ... 177