Раздел: Документация
0 ... 135 136 137 138 139 140 141 ... 177 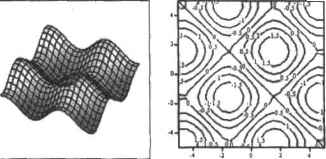 Рис. 13.9. Поверхность и контурный график функции f(x,у)=sln[x)+aln(y) Итак, в качестве точки локального минимума была определена точка M-(Q,I, -0,1). Однако обе частные производные в этой точке равны косинусу соответствующей переменной и принимают значение 0.995, то есть не выполняется необходимое условие локального экстремума. Поэтому, естественно, в данной точке никакого минимума нет и бытъпе может. Так что с этом случае Minimize допустила ошибку, причем весьма грубую. Анализируя результаты проделанной работы, можно сделать вывод: следует стараться не услояснять решаемую с помощью Mathcad проблему. Tax, введение дополнительного условия в рассмотренном выше примере, привело к получению довольно грубой и глупой ошибки. В то же время совсем несложно доказать, что вычислить экстремум, удовлетворяющий условию к+у-0, нельзя (подумайте, почему?). Впрочем, если записать более согласованную систему, то функции экстремумов придут все-таки к правильным выводам. Пример 13.0. Найти условный экстремум функции f(x,y)=sin(x)-sin(y) при х+у=0 В заключение еще раз повторю, что к результату работы функций Maximize и Minimize следует относиться предельно осторожно и по возможности проводить проверку, иначе частые ошибки практически неизбежны. f(x,y) :=sm(x) -sin(y) x:=lу:=1 Given х+ у = 0 13.4. Линейное программирование (решение задач оптимизации) Линейным программированием называется раздел математики, который занимается проблемами минимизации линейной функции конечного количества переменных. удовлетворявши набору ограничений в виде линейных уравнений или неравенств. Линейное программирование является основным аппаратом в теории оптимального принятия решений в первую очередь в задачах экономического планирован ия. Впервые задачи линейного программирования сформулировал советский математик Л. В. Канторович, за что впоследствии получил Нобелевскую премию по экономике, В настоящее время для решения задач данного типа разработано сложнейшее про-фаммное обеспечение, позволяющее эффективно анализировать входные данные больших объемов и получать достоверный результат. В общем виде задача линейного программирования формулируется следующим образом: необходимо определить неизвестные величины х,, ..х, при которых функция fXx) = Cj X, +Vx; + ... +cn.xn называемая целевой, принимает минимальное значение при условии принадлежности переменных некоторой области, определяемой системой линейных равенств »Н Х1+а12Х2+-+а1ПХП=Ь, а3х1 + в22-хг+ .- + an2-xn = b! emi-xi +w2+ "+anmxn=bm и их иеотрицатености; х,*0 х3г0XjjO Описанная срорму.игровка задачи линейного программирования называется канонической. Именно к такому виду должна быть приведена задача, чтобы для ее решения можно было применить один из численных методов оптимизации. На практике же ограничения для переменных могут быть представлены в форме равенств, неравенств различных знаков н даже комбинации равенств И 11еравснств. Однако все они путем несложных приемов сводятся к ограничениям двух видов: равенствам н условиям неотрицательности. Наиболее распространенным и универсальным методом решения задач оптимизации является так называемый симплекс-метод, позволяющий найти оптимальное решение за (2-3)т итерации, где га — количество равенств-ограничений. Решение задач линейного программирования в Mathcad имеет несколько тонкостей, связанных прежде всего с заданием условия. В остальном же проблемы, которые могут возникнуть прн работе с ними, связаны со слабостями функций экстремумов Maximize и Minimize и будут характерны для всех задач, в которых функции эти используются. Поэтому останавливаться на них, ввиду того, что способы разрешения таких трудностей были весьма подробно рассмотрены в двух предыдущих подразделах, мы не будем. Следуя избранному сгилю, изучим решение задач линейного программирования, просто найди условие оптимизации конкретной практической задачи. Одним из самых распространенных типов задач линейного программирования являются задачи, связанные с минимизацией транспортных или складских расходов, максимизацией прибыли за счет удачного распределения товара. Типичная задача оптимизации ставит условие приблизительно следующим образом. Пусть в районе есть три свинофермы (в колхозе * II у гь Ильича», в совхозе «Подольский» и у фермера Забутько). Предприниматель Иванов хочет купить у них мясо и перерабо- тать его в тушенку для последующей продажи службам армии. Сделать это можно на двух мясокомбинатах, расположенных в соседних районах. Мясокомбинаты государственные, поэтому и цена переработки одинакова, И совхоз, и колхоз, и фермер согласны продать свинину по одной и той же цене. Проблема выбора переработчика в том, что один из них, расположенный ближе к производителям, может принять очень ограниченный заказ (всего 20 т). Другой же, хоть и может переработать любое количество мяса, находится довольно далеко. Перевозка же свиней на 1 км увеличивает стоимость сырья на $1,2 иа каждую тонну. Задача состоит в том, чтобы распределить купленных свиней между перерабатывающими предприятиями так, чтобы транспортные расходы были минимальными Информацию о количестве мяса, купленного у каждого производителя, и расстоянии от последних до каждого из мясокомбинатов можно узнать из табл. 13.1. Таблица 13.1. Донные о поставщиках и переработчиках
Итак, попробуем найти для предпринимателя оптимальный путь распределения сырья с помощью Mathcad. 1. Для начала представим исходные данные в наиболее приемлемом для обработки программой виде - как матрицы или векторы. В первую очередь зададим вектор F распределения сырья и вектор МК объемов возможной приемки данного сырья мясокомбинатами. Очевидно, что, так как первый мясокомбинат ближе ко всем производителям, то везти на него сырье выгоднее, поэтому загрузить его следует по максимуму. То мясо, которое не сможет взять первый мясокомбинат, придется везти на второй.  SF = 55МК=55 2. Далее зададим матрицу расстояний, всфокахкоторойбудутрасположены соответствующие расстояния от производителей до данного мясокомбината На этом же этапе определим коэффициент транспортных расходов, равный увеличению стоимости продукуии при перевозке тонны сырья на 1 км: TR := 1 2 (32 12 54 RasP := 160 144 \99) 0 ... 135 136 137 138 139 140 141 ... 177 |












