Раздел: Документация
0 ... 134 135 136 137 138 139 140 ... 177 При использовании стандартной записи функции Maximize при начальном приближении х-3 система выдает значения максимума, более близкого к згой точке: 7 з ft» :=-х + 4х - Зх х;=3 Maximized,х) - 1.077 Но прн использовании записи с вычислительным блоком при этом же приближении мы сможем получить значение и из отрицательной области. Для этого требуется лишь ввести ограничения на положительные величины точки максимума под ключевым словом Given: х:-3 7 3 fi» :=-х + 4х - Зх Given х < О Maxiraize(f, х) = -0.51 Впрочем, если взять начальное приближение, равное, например, 10, то никаких экстремумов не будет найдено вообще. Связано это. прежде всего, с очень высокой скоростью возрастания функции (то есть производная принимает слишком большие для эффективной работы численного алгоритма значения). Равно как и при стандартной записи, функции экстремумов с вычислительным блоком крайне чувствительны к величинам начальных приближений. Так, попробуем найти максимумы рассматриваемой функции, выделив интервал их локализации: х:=0х:=1 7 37 3 f(x):=-x + 4х -3-хf(x);=-x + 4х - 3-х GivenGiven -3<х<3-3<х<3 Maximize(f,x) - -0J1Maximize(f,x) = -3 При начальном приближении х-0 один из локальных максимумов был найден верно. Но при попытке определить экстремум на положительной области (х-1,077) был выдан довольно неожиданный результат (х—3), хотя точка приближения была выбрана предельно близко к нему. Фактической ошибки, конечно, при этом допущено не было, так как на левой границе выбранного интервала функция действительно принимает свое наибольшее значение. Но как же в такой ситуации определить именно локальный максимум? Испробовав десяток начальных приближений, приходим к выводу, что при данных условиях найти правый экстремум весьма проблематично, хотя при стандартной записи без каких-либо дополнительных условий функция Maximize при использовании той же начальной точки находила его очень легко. Таким образом, делая вывод, можно утверждать, что, если на интервале расположено несколько локальных экстремумов, лучше не рисковать и использовать стандартную запись функций Maximize и Minimize. Если же экстремум только одни, то использование вычислительного блока— очень эффективный и простой способ определения максимума или минимума Но в любом случае проверка результата обязательна. Грубой ошибкой функций Maximize и Minimize является и то, что в качестве экстремумов они выдают абсциссы всех точек, в которых первая и вторая производные имеют нулевые значения, однако, как вы помните, для ряда функций такие точки могут быть и не экстремальными. Пример 13,6. Рассмотрим функцию (рис. 13.7) 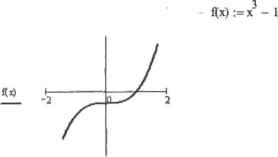 Рис. 13.7. График рассматриваемой функции Функция эта возрастает на всем промежутке своего определения и никаких экстремумов не имеет. Но в точке х-0 ее первая производная (3xJ) и вторая производная (6х) равны 0. А это означает, что алгоритм Mathcad мало того, что определит ее в качестве точки экстремума, так и к тому же отнесет ее одновременно и к минимуму, и к максимуму; х:=0 Maximized,х) °= 0 Minimize(f,x) = 0 13.3.2. Экстремум функции нескольких переменных Различие между поиском экстремума функции одной переменной и функции нескольких переменных приблизительно такое же, как между решением уравнения с одним н ei [эвесткьш и системы уравнений. То есть если максимум или минимум функции, зависящей от одной переменной, можно определить, найдя нули ее производной, то для того чтобы уанать координаты точки экстремума функции нескольких переменных, придется решить систему уравнений (необходимым условием существования в данной точке экстремума функции нескольких переменных является равенство всех ее частных производных 0). Функции Maximize и Minimize могут быть использованы и для нахождения экстремумов функций нескольких переменных. Пример 13.7. Найти экстремумы функции двух переменных (рис. 13.8) Рис. 13,а. График исследуемой функции двух переменных Функция эта симметрична относительно своих переменных, то есть ее частные производные равны при любых значениях переменных. Из графиков следует, что она имеет локальный минимум и локальный максимум. Найти их можно очень просто и без помощи компьютера: частные производные равны Зг*- 5 (г-х, у), откуда локальные экст ремумы должны иметь координаты (1.291,1.291) или (-091,-1.291). Попробуем теперь их найти с помощью функций Maximize и Minimize. Результат полностью соответствует расчетам, сделанным нами ранее. Аналогично функциям одного переменного. Maximize н Minimize могут быть встроены в вы-чнелитслькый блок. При этом можно вводить целый ряд допачнителыгых условий, что может быть весьма удобно для определения нужного значения экстремума. Однако, задав какие-то дополнительные условия, нужно быть очень внимательным к результату. Пример 13.8. Рассмотрим функцию (рис. 139} f(x,y) :=«n(x) + sin(y) Функция эта имеет бесконечное множества минимумов и максимумов. Попробуем, однако, найти минимум из того условия, что х+у-О: flXy) :=*in(x) + ein(y) fi>.y) :-Х3 + у3 - [S(x + у) + 4] 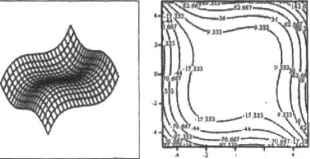 л 4 i з « Г г Given х + у = О 0 ... 134 135 136 137 138 139 140 ... 177 |












