Раздел: Документация
0 ... 132 133 134 135 136 137 138 ... 177 Глядя на график, можно сделать вы во л о том, что первое неравенство было решено системой верно: Г(х)>0 на промежутке (—*, -3). а вот со вторым неравенством Mathcad справился немного хуже - полученный результат мрея частично; f*(x)<0 на промежутке (-3; 0)\j (0; •»). Исходя из этого, в интервале (-«; -3) график исследуемой функции является вогнутым, в интервале же (-3; 0) и (в; ~) - выпуклым. При переходе через точку х"-3 вторая производная меняет знак, значит, х--3 является точкой перегиба графика функции. Обратите внимание, в данном стуча* достаточное условие точки перегиба не выполняется, поскольку в ней вторая производная равна не 0, а бесконечности. Тем не менее поведение функции второй производной (которая не является непрерывной) я окрестности этой точки дает нам право считать ее точкой перегиба (что, в общем-то. очевидно из графика). При х-0 вторая производная также обращается в бесконечность, но не меняет знак в окрестности данной точки, поэтому при х-0 перегиба нет. В-седьмых, найдем асимптоты графика функции Асимптотой кривой называется прямая, к которой неограниченно приближается точка этой кривой при неограниченном удал ei гни от начала координат. Исследуемая нами функция не имеет вертикальных венлпттот, поскольку непрерывна на всей числовой оси. Невертикяльные асимптоты будем искать в виде y-bt+b (рис, 13,3): Ях) k := Lim — -» 1Ь:=> lira (fl(x) - к-х) -> 1 \ —> oo хX —► do 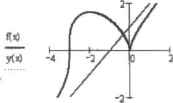 Рис. 13.3. Асимптота у=х->-1 графика исследуемой функции у-х* 1 является наклонной аоипттотой. Расстояние от нее до точек графика функции неограниченно уменьшается с ростом х: lira [fi;x)-(x+ I)] О X-» =0 В-восьмых, найдем предельные значения функции на концах области определения. lim (х+3)х -юоlira V(x+3)X -»« X—► - сох.—► во Строго говоря, предельное значение функции на левой транше области определения равно не » а ~, в чем легко убедиться исходя из графика. Проведенное нами исследование функции в очередной раз доказывает, что полностью доверять результатам, полученным при символьных расчетах, нельзя: проверка любого из них по графику обязательна- 13.2. Исследование функций нескольких переменных Как и в случае функций одной переменной. Mathcad существенно облегчает исследование функций многих переменных благодаря возможности построения описывающих их поверхностей и линий уровня, с помощью которых доказать непрерывность функции, найти экстремумы, седловые точки, а также точки или линии разрыва намного проще. В данном разделе мы разберем, как средствами Mathcad можно определить экстремумы функции двух переменных. Пример 13.2. Найти экстремум функции двух переменных fitx,y) = e"XV(3x2 + y2) Пскггроить линии уровня функции Построим в первую очередь линии уровня исследуемом функции (подробно о способах задания поверхностей и контурных графиков рассказано в гл. 6) (рис. 13Л): цХу):=Г*г~у2(зх2 + у2)  Рис. 13.4. Линии уровня исследуемой функции двух переменных Необходимым условием экстремума функции нескольких переменных в точке (х0, у„) является равенство нулю ее частных производных данной точке. Достаточное условие экстремума заключается а следующем Пусть в точке (х,, у) f ,(х у,)-0, f г(х у,)*-0. и функция имеет в этой точке непрерывные частные производные второго порядка: FjJb У.У-А riy(v у,Иу*.. у,)-Вrjfr у-С Д-АС-гР Тогда еслн Д>0, функция имеет экстремум я точке (х,. уй): максимум при А«;0 н минимум при Л>0. Если д<0. экстремума в точке нет — она является селловой. Исследовалше функции двух переменных на экстремум также проведем па пунктам. Во-первых, найдем частные производные функции: —fi>,y)-*-2y.e~*~y (з-х2+ у2)+ 2-уе"у2 эу -»Тх,у) -» -2-х-с~* ~у (3-х2 + у)+ 6х-е х ~у 5х Во-вторых, найдем критические точки функции, решивсистему уравнений f ](xll,yn)-0, f (х„ у„)Н): Given -2-хе-1.(з-х2 + у2)+ 6*<ГО 2 2 ✓ -> ->ч22 . -х-у /12 2\ — х-у „ -2-у-е J (3-х + у 1+ 2-у-е =0 (ООО I -Л Find(x,y) -И Vo i -i о о ) Обратите внимание, в данном случае система нелинейных уравнений была решена символьно. К сожалению, в Mathcad это возможно далеко не всегда, поэтому в случае, если критические точки символьно определить не удастся, для каждой из них в отдельности придется задавать начальное приближение исходя из контурного графика. И - третьих, найдем частные производные второго порядка, вычислим ИХ значения в каждой критической точке и с помощью достаточного условия сделаем вывод о наличии экстремумов (для экономии места исследуем две точки из полученных пяти). Я2Я ЯЯ2 A(x,y):«-2-j4*.y)В(х.у):«2-2-Чх,У>С(х,у>2-j«x.y) дхдхдуду А(1,0)-С(1,0) -В<],О)2 = 6.496А(1,0)-~4.415 В точхе (1,0) д---и и А<0. значит, это точка максимума .Аналогичным образом можно доказать, что (-1,0) является точкой максимума, в (0.0) - точкой минимума функции. Исследуем точку (0, 1). А(0,1)-С(0,1) - В(0,1)2 - -2.165 д оказалось отрицательным, следовательно, в данной точке экстремума нет, она является седло вой. То же самое можно утверждать, исследовав точку (0. -1). В-четвертых найдем значения функции в точках экстремума: fl0,0)->0f(l,0) 3-е" 1 fH.0)-»3c 1 0 ... 132 133 134 135 136 137 138 ... 177 |












