Раздел: Документация
0 ... 129 130 131 132 133 134 135 ... 177 тем, определение- необходимого Кол si честна членов разложения — это довольно нетривиальная задача. К счастью, имеются удобные формулы, которые позволяют оценить порядок остаточного члена разложения (погрешность будет определяться именно этой величиной). Широко известны формулы для остаточного члени в форме Лафатгжз, Коти, Пеано. Менее известна формула остаточного члена в интегральной форме. В рамках нашей задачи наиболее удобна именно она: Здесь л — количество членов разложения, Р1" IJ(t) - производная порядка н+1 разлагаемой функции, t — переменная подынтефальпой функции (она исчезает после проведения шгтефирова-ния), а — точка разложения (в нашем случае тс/3), х - точка, в которой вычисляется зиачение функции (в нашем случае 1). Нам нужно найти минимальное п, при котором остаточный член по модулю окажется меньше Ю-1*. Увы, но если написать на основании формулы для К.„(х) уравнение относительно tvroem не удастся решить ни аналитически (оно будет слишком сложным), ни численно (R (х) не является непрерывной функцией от п). Не получится решить его и фафнчески, так как порядок величин слишком мал (не поможет даже использование логарифмическое шкалы). Так что остается одно: подобрать п вручную. Для этого представим формулу для остаточного члена в виде функции от п и х: Подбираем п для точки х-1. Расчет значения функции R(n.x) необходимо выполнить аналитически, а затем пересчитать результат в десятичную дробь. Почему? Во-первых, при атом будеи достигаться куда большая точность, чем при численном расчете. Во-вторьгк, это позволит райо тать с очень малыми величинами (при численном расчете они будут округляться до 0). В-третьих, главное, в выражение R(n.x) входит Производная порядка н +1. Л гак как численно можно рассчитать производную лишь до пятого порядка, то численно значение R(n,x) можно найти лишь при л<5. Итак, мы должны разложить синус в ряд на шести-семи членов (не пяти, так как нужно учесть и нофешность при проведении арифметических расчетов); Г* 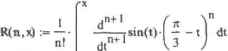 3 R(5,1) float,40 -> -1.3243528984249241820967802402010 г"1 Н» .= sin(x) series . х = - ,6 -», — 1 +• - х---jt U —3 х---и I i) U %\ j J * \ -i ). 1 Находим значение синуса в точке х*=1, отвечая но вопрос задачи: цЧ) =0.8414709848 Проверяем верность ответа с помощью встроенной функции Mathcad sin: sin(l) = 0.8414709848 Ответы сошлись. Следовательно, задача была решена нами абсолютно верно. Особенностью рядов Тейлора является то, что они (при фиксированном количестве членов) тем лучите приближают функцию, чем ближе точка располагается к точке разложения. Соответственно, чем дальше точка находится от точки разложения, тем больше членов ряда придется просуммировать, чтобы достичь нужной точности. В принципе, сколь угодно точное значение футгкции можно найти в сколь угодно удаленной от точки разложения точке — но количество членов ряда Тейлора, которые придется для этого просуммировать, может быть весьма значительным, Т\ро-демонстрируем это на примере. Посмотрим, сколько нужно взять членов ряда, полученного разложением синуса в точке а-п/3. чтобы вычислить значение этой функции в точке х-2 с точностью до 10°: R(12,2) Поел,40 -> 3.021 IO56 5 23608O7O8392156750O0495 10~И Как и следовало ожидать, с удалением отточки разложения длина аппроксимирующего ряда возросла. Посмотрим.будет ли результат точен до Ютознака.если мы возьмем 13 членов разложения: tT2) = 0.90929 74268влл(2) = 0.9092974268 Возьмем еще более удаленную точку х-10: R(40,]0) float,40 -* -2.931460350764340735769938368089913258176-10~U f(10)= -0.5440211109sin(10)= 0.5440211109 Чтобы вычислить в этой точке cmryc с нужной точностью, придется просуммировать 41 член разложения! Представляете, как сложно было бы выполнить эту работу на бумаге? Делаем вывод: очеш, важно правильно выбрать точку разложения — это может уменьшить объем вычислительной работы на порядок. Заканчивал обсуждение данной задачи, приведем график функции, аппроксимирующей синус, которая представляет собой ряд из 41 члена (рис, 12.2), Посмотрите, на каком широком промежутке полином ведет себя точно так же. как синус. Удивительно, не правда ли? 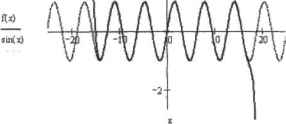 Рис. 12.2. Кривая синуса и график аппроксимирующего ее полинома Помимо приблизительного нахождения значений функций в неаналитических точках, ряды Тейлора активно используются при вычислении пределов. Данный подход хорош своей универсальностыо и простотой, поэтому именно его использует символьный процессор Mathcad при подсчете пределов. Приведем и мы пример такого применения рядов Тейлора. Пример 12.11. Нахождение пределов с использованием разложения в ряд Тейлора Пусть стоит задача без применения оператора Inn найти следующий предел: cos(x) 2 lim - *-» 0 х3 sin(x) Чтобы найти данный предел, нужно раскрыть неопределенность -1/0, что довольно непросто сделать посредством стандартных средств Однако если разложить функцию в ряд Тейлора, задача будет решена довольно просто: -х3 в - cos(x) , „ 1 1 г 29 л -вепек,х,9 ->---х +-*х ljb12 180 30240 X Stn(X) Полагая х равным 0, находим, что предел будет равен 1/12, Этот же ответ будет выдан и оператором lim Mathcad: lim cos(x) 12 0 x sin(x) Приведем примеры расчета с использованием ряда Тейлора еще двух пределов: lim х-* 0L х-(«п(х)-х) cos(x) + — 2 , 1 - I t x(sin(x)-x) aeries, x, 5 —* с - [ t lim x-» 0 в -1-х с -1-х series, Х.З -> С 12.6. Разложение функций в ряды Фурье Разложение в ряд Тейлора периодических функций - это не очень эффективный ход, так как пин этом хороший уровень аппроксимации будет достигнут лишь а окрестности точки разложения. При отдалении же от нее приближение будет плохим, хотя участки 0 ... 129 130 131 132 133 134 135 ... 177 |












