Раздел: Документация
0 ... 127 128 129 130 131 132 133 ... 177 ными знаками поел»запятой. Это означает, что функция должна быть аппроксимирована с точностью до 7-8 знаков после запятой, так как два-три разряда будут потеряны за счет погрешности как численных методов, так и компьютерной арифметики. Чтобы найти о всхода на этого условия, подберем для нашего функционального ряда мажорантный числовой ряд (это такой ряд, члены которого всегда больше или равны соответствующим членам данного ряда): 4 cos[(2n + 1)-х] 4 1 * (2п + t)2 rt <2n + I)2 Очевидно, что еслн о взять таким, что сумма мажорантного ряда вычислится с точностью до 8-го знака, то такой же или более высокий уровень точности будет достигнут при суммировании п членов ряда, задающего f(x)( так как он быстрее сходится) Л гак как иыбрлнный мажиран гный ряд является абсолютно сходящимся числовым рядом, то погрешность вычисления его суммы не превышает величины первого отброшенного члена. На основании этого свойства можно найти п, решив соответствующее уравнение: I " (2п + I)2 .-8 soh/с, в. float,5 5641.6 -5642.6J J !так, чтобы аппроксимировать f(\) < гочиостьЬДи Я-и злака иен-лс .мниrot, СЛЕДуе! Просуммн ровать порядка 5600 член ов задаюшего ее ряда. Согласитесь, это доволыго много (разумеется для человека: для компьютера это мизер). Вообще, тригонометрические ряды сходятся намного медленнее, чем ряды Тейлора, что долго ограничивало их использование в приблизительных расчетах, Задаем функцию, аппроксимирующую f(x); 5642 4 x-i cos[(2n + 1)-х] я 4 т—I а =0 Численно подсчитываем производную и интеграл: (2n + 1) 1 dx 1 г xdx= 4,9348 Строим график (рис. 12. L). Обратите внимание, что на это потребуется в общем не очень много времени, что удивительно с учетом того, сколько точек должно быть посчитано. 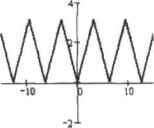 Убедиться в том, что задача была решена верно, можно, зная, ЧТО ряд, задающий К», есть не что иное, как результат разложения в ряд Фурье фунюши р(х)-х на промежутке от -я до я: 1 -р(х) = 1 dx р(х) := М p<x)dx = 4.9348 12.3. Произведения Полностью аналогично сумме ряда можно вычислить произведение его членов, Для этого нужно воспользоваться специальным оператором Iterated Product (Результат произведения), который, помимо нажатия кнопки панели Calculus (Вычисления), можно ввести сочетанием клавиш Ctrl+Shift+Э: п В Mathcad можно вычислять конечные (численно и аналитически) и бесконечные (только аналитически) произведения. Наиболее интересны сходящиеся бесконечные произведения. Для примера приведем несколько подобных произведения. Пример 12.5. Вычисление бесконечных сходящихся произведений Произведения, сходящиеся к числам: со у.00 п ( п к = 2 (*~ !)-(*+ 2) к <К I I) Произведения, сходящиеся к функциям (приведенные произведения могут использоваться для вычисления значений синуса и косинуса вместо рядов Тейлора): п I ] ь2 2 sin( I) п k-i L (2к- 1)2-тс2 cos(l) Произведение, позволяющее вычислять число (С П к= 1 4 к Конечные произведения не столь изящны, как бесконечные, однако они куда более важны для практики. Они могут использоваться при решении таких задач, как вычисление биноминальных коаффшшеитов, геометрического среднего, определения значений различных математических функций к констант, Пример 12.6. Вычисление конечных произведений Функция, находящая биноминальные коэффициенты (число сочетаний из о по к): 12.4. Ранжированные суммы и произведения * 405 к-1к binom(n,k) := J £ (n-i) + J bmom(5.3>= 10 bmom(2,1)2 Функция, позволяющая определять значения синуса. Аналогична встроенной функции sin: Помимо стандартных, широко распространенных в математике операт«[юв обычного суммирования и умножения, в Maihcad есть два довольно интересных оператора так называемых ранжированных сумм (Range Variable Summation - Суммирование по ранжированной переменной) и произведений (Range Variable Iterated Product — Произведение по ранжированной перешишсОД Bhl-гти их МОЖНО Л ибо С ВД1ЙУ1И Calculus. Лмбо сочетаниями клавиш (Srrift+4 — для суммы н Shift+З — для произведения): При использовании данных операторов и первую очередь нужно задать ранжированную переменную, которая покажет, какие зпачеиггя должна принимать перемен пая цикла или произведения. Определив ранжированную переменную, ее имя нужно ввести в нижний маркер оператора. При этом будут просуммированы или перемножены нее элементы последовательности, соответствующие заданным.значениям ранжированной переменной. Если ранжированная переменная принимает только целочисленные значения, такое суммирование или умножение не имеет никаких отличии от использования простых операторов ряда. Дополнительные возможности ранжированного суммирования или произведении проявляются тогда, когда переменная должна изменяться не с целим шагом. Ко взаимозамецимы операторы суммировании и произведений всегда. Операторы ранжированной суммы или произведения обычно используются тогда, когда необходимо произвести обработку Матрицы ИЛИ вектора. В качестве примера покажем, как с их помощью можно вычислить три вида среднего: арифметическое, геометрическое и среднеквадратичное. Пример 12.7. Вычисление различных средних для выборки 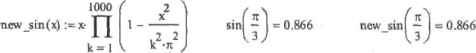 12.4. Ранжированные суммы и произведения • data :=(1 2 3 4 5 6 7 8 9 10) NN lengthtdatu) i:=0.. NN - I 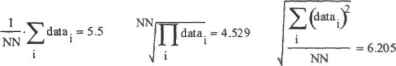 0 ... 127 128 129 130 131 132 133 ... 177 |












