Раздел: Документация
0 ... 128 129 130 131 132 133 134 ... 177 Ранжированные суммы и произведения можно вычислять и аналитически. Причем при этом не обязательно задавать ранжированную неремештую. Если в оператор ранжированной суммы или произведения в качестве переменной ввести неопределенную величину к, то ответ будет рассчитан из условия изменения переменной от 0 (или 1, если возникает ошибка деления на 0) до к с шагом 1. Пример 12.6. Использования операторов ранжированной суммы и произведения в аналитических вычислениях *-<k(k- I) (k-1)Ilk Г(к) к 11v»! 11 к(к- I) Г(к)Г(к-1) к кк Установить однозначное соответствие между результатами символьных вычислений с помощью ранжирован!гых и обычных операторов суммирования и произведения зачастую бывает не столь просто. Например, после суммирования к элементов гармонического ряда в примере 12.8 был получен результат в виде функции Psi(k). Функция .гга имеет вид Psi(x) = -ln(r(x)) dx и сама по себе лишь повторяет поведение ломаной гармонического ряда, абсолютно не совпадая с ней: сен» Р<*):= £ £ fCx):=Psi(x) k = l 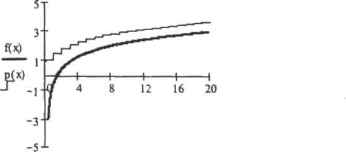 Чтобы через функцию Psi точно выразить сумму гармонического ряда, к этой функции следует прибавить специальную величину - так называемую константу Эйлера у, приблизительно равную 0.57722. Также нужно учесть, что функция Psi «отстает* от функции суммы ряда на единицу. у ;» 0,57722:=Psi(x+ J) + у к = 1 If  Hi Таким образом, результат ранжированного суммирования членов гармонического ряда был получен не совеем корректный. Однако выражение для суммы гармонического ряда в случае использования оператора простого суммирования будет определено верно: Сделаем вывод: использование операторов ранжированного суммирована и умножения в случае аналитических расчетов имеет ряд особенностей и может привести к неожиданному или даже неверному результату. Поэтому по возможности (а возможность такая есть всегда) используйте все-таки стандартные операторы ряда. 12.5. Разложение функций в ряды Тейлора С помощью символьного процессора Mathcad можно выполнить и такую важную с практической точки зрения операцию математического анализа, как разложение функции в ряд Тейлора. Для этого следует воспользоваться оператором series (Ряд) панели Symbolic (Символьные): Данный оператор содержит три маркера. В первый вводится функция или ее имя. Во второй — переменная, по которой должно быть проведено разложение. В третий -количество членов ряда (что соответствует порядку точности). По умолчанию разложение производится в окрестности 0 (то есть вычисляется так называемый ряд Маклорена). Если же ряд нужно найти для окрестности другой точки, то следует переменной во втором маркере оператора series присвоить с помощью логического равенства (Ctrl-*-) нужное значение (оно может быть как численным, так и символьным). Зачастую приходится аппроксимировать рядами функции нескольких переменных. В Mathcad найти такой ряд можно, введя в оператор series не одну переменную, а две (или любое количество). Сделать это можно, просто введя после второго маркера запятую. При этом появится еще один маркер, в котором можно задать имя второй переменной. Используя оператор series, можно произвести разложение в ряд длиной до 100 членов. t = l series ,i , —► Пример 12.9. Вычисление рядов Тейлора различных типов Разложение функции в ряд Маклорена: I 2 14 ln(x + em(x)) sencs ,х,7 —► 1п<2) t 1п(х)---х +--х + 12 1440 1SI44 а 6 Разложение функции в ряд Тейлора и окрестности точки х-а: - series.х = а,5 -* - + — (х - а) + — (х - а)2 + —-(х - а)3 + — (х - а) ха 2345 аааа Разложение о ряд Тейлора функции двух переменных: Обратите внимание на то, что ОТВсТ при использовании оператора series выводится без остаточного члена 0(.т"). Это сделано для того, чтобы результат вычислений можно было беа проблем использовать в дальнейших расчетах. Еслн же формула должна быть збгол ютно верной, то разложение нужно осуществить не посредством оператора series, а командой Expand to Series (Разложить в ряд) подменю Variable (Переменная) меню Symbolics (Символьные). При атом остаточный член будет включен в ответ, Например, при разложении f(x)-sin(x) и ряд Маклорена из пяти членов получим следующий результат: Mathcad не умеет находить формулы общих членов рядов Тейлора. Прн необходимости эту работу придется производить самостоятельно, анализируя и сопоставляя несколько первых членов разложения. Или же, в крайнем случае, можно воспользоваться справочником. В математике ряды используются прежде всего для численных расчетов, и. в частности, для аппроксимации функции в окрестности точки, в которой известно ее точное аналитическое значение. В следующем примере рассматривается влияние порядка раз* ложен ия на точность приближения функции. Обратите также внимание на то, сколь сильно влияет на результат правильность выбора точки разложения Пример 12.10. Используя разложение в ряд Тейлора, найти значение функции f(x)=sln(x) в точке х=1 с точностью до 10гм Чтобы получить максимальную точность при минимальном количестве членов в ряду, мы должны произвести разложение в окрестности точки, для которой характерно, с одной стороны, то, что для синуса в ней известно аналитическое значение, а. с другой, то, что она находится близко к точке х-1. Наилучшим образом атим условиям удовлетворяет точка х-к/3. С тачкой разложения мы определились. Но сколько член** должно быть в ряду, чтобы была догцикута желаемая точность? Очевидно, что необходимое количество членов разложения зависит от близости точки, в которой должно быть вычислено значение функции, к точке разложения. Чем паи будут дальше друг от друга, тем больше членов придется рассчитать. Также, несомненно, влияние оказывают и особенности поведения функции а окрестности точки разложения, В об- I sin(x + у) series,х 0 ... 128 129 130 131 132 133 134 ... 177 |












