Раздел: Документация
0 ... 131 132 133 134 135 136 137 ... 177 Поскольку алгоритм исследования функции включает в себя большое количество пунктов, разберем каждый нз них ло отдельиостн, прибегая, в случае необходимости, к теоретическим пояснениям. Для обпегчения поставленной задачи построим и первую очередь график функции (рнс 13.1>. Заметьте, При проведении исследования на бумаге такой возможности у вас нет. 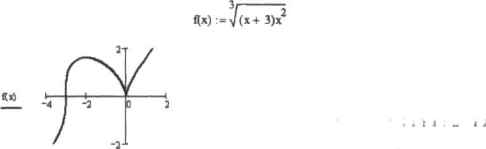 Рис. 13.1. График исследуемой функции Во-первых, найдем область определения и область значений функции, X может принимать любые значения (в выражении функции отсутствуют корни четной степени н знаменатель), поэтому функция определена на всей числовой осн. Очевидно, область значен и й функции принадлежит промежутку (—»,«). Во-вторых, определим, является ли функция четной, нечетной или периодической. Видно, что график несимметричен относителыш оси ординат и начала координат, значит это функция общего вида. Приведем аналитическое подтверждение. ill п» -* [(а + З)»2]f(-*) -* [(-а + 3).а2]-{(а) -> -[(а + 3)-а2] Как видно из полученных выражений, условия четности (f(-a)-f(a)) и нечетности (f(~a)--f(a)) не соблюдаются, значит, это функция общего вида. Докажем непериоличность исследуемой функции. Функция является периодической, еслн для любого х существует такое действительное число Т, отличное от нудя, что f(x+T)-f(x). Доказательством периоднчности/аеперио личности функции является нахождение величины Т нэ уравнения f(x+T)-f(x). Если Т является действительным числом, функция периодична. В случае не-периодичноетн Т будет являться функцией от х. Гil 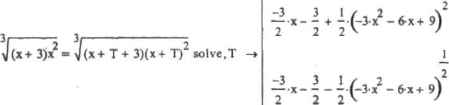 о П .11 решении уравнения f(x+7>»H» отиоагтельио Т мы получили три значения. По определению Т*0. остальные же выражения зависят от х, следовательно, функция является непериодической. В-трегмгх, точеж разрыва фу шипя не имеет, поскольку непрерывна на промежутке (-•»; ~>). В-четвертых, наИдсм точки пересечении графика функции с осями координат. J-5 (Х+ 3)* )х solve,х О График функции пересекает ось Ох а точках (-3; 0), (U; 0). График функции пересекает ось Оу и точке (0:0). В-нигыч. определим точки экстремума, значения функции и яТИя точках, а также интервалы возрастания и убывания функции. Необходимым условием существования зкетрсыума в точке xD является равенство нулю или несуществование {равенство бесконечности) производной и данной точке. Достаточным условием существовании акгтреыума в точке ха является смена знака приизвилиoil при переходе через точь\ я+ 2Я+ 2 —Дх) simplify dx solve,х -+ -2 t(x+Vx2] [(x+ Э)х2] llpiiii iiHi.sii.in pauua нулю при x=-2, при x—3 и x-Q она обращается а бесконечность. Значит, данные критические точки янляются точками перегиба или зкетреыума. Чтобы проверить последнее утверждение, найдем интервалы возрастания и убывания функции. Для этого вспомним достаточное условие монотонности функции, утверждающее, что дифференцируемая к вот рас- нюним I voi.iHamm.iM) в интервале (а, Ь) функция f(x) имеет во всех точках этого интервала неотрицательную (неположительную) производную. х*- 2 > 0 solve,х [(х+3)-х2] х+ 2 <- г [(х+ 3)-х2] <: 0 solve.х х < -3 (-3 < х)<(х< -2) О < х х<-3 L(-2<x)(x<0)J Как вы помните, но избежание ошибки при речненнп неравенств в Mathcad полученный резу.ть-тат следует об«за1слыю проверять (й фафнку (подробно О (правилах интерпретации результатов, полученных при решении неравенств, см. в г л 9). В нашем случае решение обеих неравенств было найдено с учетом того, что Я точке х--3 функции производной терпит разрыв, однако с помощью графика мы можем укчзатькор-ктиые промежутки л мкопостояцетва исследуемой функции: н интервале ( —. - 2) U (0; -) функтшя ширштагг, в интервале (-2: 0) - убывает. Итак, при переходе через точку х--2 производная меняет знак с плюса на минус, значит, в данной точке функция имеет максимум: При переходе же через х-0 знак производной меняется г. минуса на плюс, следовательно, в данной точке расположен минимум: Заметьте, при х--2 экстремум гладкий (Р(-2)-0). а при х-0 — острый (F(0)~*°). При х--3 экстремума нет, поскольку знак производной сохраняется. Поведение функции в этой точке требует дополнительного исследования. Взглянув на график, легко убедиться в том, что Х--3 является точкой перегиба, однахо это необходимо подтвердить аналитически, определив шгтервалы вогнутости и выпуклости. В-шестых, найдем интервалы вогнутости и выпуклости рафика функции, а также точки перегиба. Достаточным условием вогнутости (выпуклости) кривой па промежутке (а; Ь) является положительный (отрицательный) знак второй производной на данном промежутке. Промежутки монотонности функции второй производной можно определить из соответствующих неравенств, проверяя результаты по графику (рис. 13.2). t\-2) = 1.587 fl[0) = 0 —sfl» simplify -> -2 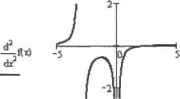 Рис. 13.2. График функции второй производной -2 > 0 solve,х -* х< -3 2 х<-3 -2 < 0 solve,х -* (х<0)-(-3<х) 2 О < х 0 ... 131 132 133 134 135 136 137 ... 177 |












