Раздел: Документация
0 ... 137 138 139 140 141 142 143 ... 177 14.1.1. Решение дифференциальных уравнений с применением преобразования Лапласа Если дифференциальное уравнение, которое вам нужно решить, имеет постоянные коэффициенты, то предельно просто можно найти его корни, используя преобразование Лапласа. Математический смысл преобразования Лапласа заключается в установлении взаимнооднозначного соответствия Между функцией действительной переменной f(t) (в терминологии операционного исчисления — оригиналом) н некоторой функцией комплексной переменной F(s), называемой изображением. Функция F(s) определяется равенством, которое получило название тгтеграла Лапласа: Преобразование Лапласа широко используется В связи с тем, что многие математические операции проше проводить над изображением, чем нал оригиналом (например, дифференцированию в оригинале соответствует умножение в изображении). Преобразование Лапласа переводит дифференциальное уравнение в соответствующее алгебраическое, аналитически решив которое и применив к нему операцию обратного преобразования Лапласа, можно получить решение ОДУ н общем виде. Именно эту идею мы и используем для того, чтобы найти корни дифференциального уравнения с постоянными коэффициентами (если они будут зависеть от каких-то функций, то, скорее всего, символьный процессор просто не сможет решить полученное алгебраическое уравнение — если, конечно, системе удастся провести само преобразование). В принципе, возможности решения ОДУ н систем ОДУ с помощью преобразования Лапласа довольно ограничены, на что есть вполне объективные причины. Интеграл Лапласа является несобственным и сходится лишь в том случае, хогда функция f(x) удовлетворяет следующим условиям: □f(x), равно как и ее производные, непрерывна для всех неотрицательных х, однако на любом конечном интервале допускается наличие конечного количества точек разрыва 1-го рода, в которых это условие не выполняется; □при х<0 функция принимает нулевые значения: f(x)=0; U f(x) возрастает медленнее экспоненциальной фуплеции Me". При х>0 существуют положительные М и а. при которых выполняется tiepaBi!itcinojf(x)<M-e"\ Несмотря на довольно большое количество ограничений, с помощью преобразования Лапласа можно найти корни практически всех дифференциальных уравнении, которые могут встретиться в практикуме но высшей математике технического или гуманитарного вуза. Убедимся в этом на конкретных примерах. Пример 14.1. Найти корни неоднородного дифференциального уравнения второго порядка Х"+4Х=12cos(2t) Приступая к решению уравнения, получим, прежл* всего,.его изображенное помощью прямого преобразования Лапласи. Для этого используем специальны ft оператор 1ар1асс(Лйнлиса) панели Symbolic Символьные): F(s)= f(x).exp(-s)dx J0 laplace.i —v В левом маркере этого оператора должно быть определено преобразуемое выражение (обязательно без «-», то есть все члены из правой части уравнения должны быть перенесены в левую), в правом - переменная, по которой будет осуществляться преобразование (а нашем случав - ty. -=-jX(t) + 4X(i) - 12cc*(2t) laplace,t -> j(»laplace(X(t),t,s)-X(0))- 14-0 +4-laplace(X(l),t,s)-12- di (•4 Далее следует упростить полученное громоздкое выражение. Для этого переменную laplace(X(t),t3) (которая соответствует корню ОДУ) заменим, например, на г, более воспринимаемую визуально. Кроме того, а изображении присутствует довольно странное определение начального условия л.чя первой производной: "t 4- О 1х(о dl Проводить дальнейшие преобразования при налички такого рода элементов невозможно, поэтому введем в выражение обыч1гую константу, например ХО. и изменим обозначение начального условия для функции с Х(0) нз ХО. В результате получим в • (в z - ХО) - XX) + 4-z- 12 (Ч После того как изображение ОДУ приведено в приемлемый для дальнейших операций вид, его нужно разрешить относительно 7 Для этого воспользуемся пи»ци»лшии оператором символьного решения уравнений solve пнисли Symbolic (Символьные): •(i-X0)-X0+4-i- 12. solve,z -> ( ) Чтобы получить решение дифференциал ьного уравнении, к полученному решен ню-изображению нужно применить операцию обратного преобразования Лапласа. Сделать это можно с помощью оператора invlaplace панели Symbolic (Символьные): (i3 Х0+ 4-е Х0+ 92 ХЮ+ 4. Х*0+ 12- <) invlaplace., s li sin(Z -1) + - • XX) sin(2 i) + ХО. cos(2* t) 2 В полученном громоздком выражении желательно привести л сдобные слагаемы с, что можно сделать, задействовав оператор collect панели Symbolic (Символьные): 3- £ sra(2-1)+ - - ХТ>- «п(2-0 + хсь сс*(2 t) collect,sin(2 2 йп(2 t)+ XO. cos (2-1) Константы XO и XO входят в независимые произвольные постоянные, определяющие вид искомой функции. По сути, ХО и ХО есть начальные условия. Если .шлать их численно, мы получим задачу Коши, которая, как известно, имеет единственное решение. Параллельно записав полученное выражение как функцию от t, можно построить соответствующий график (рис. 14.1). Х0:=0 xtj;= 1 X(t) О 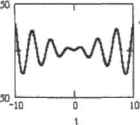 Рис. 14.1, Интегральная кривая аналитического решения ОДУ Как вы уже убедились, с помощью преобразован ия Далласа можно найти корни уравнения со специальной правой частью, подобного рассмотренному нами. С решением однородных уравнений приведенным способом Mathcad справляется ничуть не хуже. Уже при решении уравнений второго порядка приходится оперировать огромными выражениями. Как же поступить, если перед нами стоит задача найти корни уравнения высшего, например, 4-го порядка? Ведь выражение, полученное при попытке преобразовать подобное уравнение, вряд ли попадет даже в самое широкое поле зрения. В этом случае придется воспользоваться свойством линейности преобразования Лапласа, благодаря которому можно значительно упростить решение дифференциальных уравнений высших порядков. (Например, для линейной комбинации функций ау(х)+Ь/(х) существует аналогичная линейная комбинация их изображений: Пример 14.2. Решить линейное однородное дифференциальное уравнение yv-4y"+6y"-4y+y=0 Производим над функцией y(t) и каждой иэ ее производных, присутствующих и уравнении, преобразование Лапласа: =y(t) lapbce.t 1 • (I • laplaee(y(t),l.») - у(0)) -
1 4- О 3 J! dJ 0 ... 137 138 139 140 141 142 143 ... 177 |












