Раздел: Документация
0 ... 139 140 141 142 143 144 145 ... 177 При преобразовании Фурье операция дифференцирования переходит в умножение на независимую переменную. Другими словами, если F(y) — изображение функции f, а С(у) — функции f, то G(y)--iy-F(y). К функции f(x) предъявляются следующие требования: она должна быть гладкой (кусочно-гладкой) и абсолютно интегрируемой на всей числовой оси. Как известно, общее решение линейного неоднородного уравнения есть сумма общего решения соответствующего однородного уравнения и частного решения неоднородного уравнения. К сожалению, с помощью преобразования Фурье нельзя найти общее решение однородного дифференциального уравнения, однако этим способом можно легко получить частное решение неоднородного уравнения любого порядка, не оперируя громоздкими выражениями, как в случае применении преобразования Далласа. Общее же решение однородного уравнения можно найти, вычислив корни соответствующего характеристического многочлена. Чтобы продемонстрировать преимущества использования преобразования Фурье, рассмотрим конкретное уравнение. Пример 14.4. Проинтегрировать линейное неоднородное дифференциальное уравнение yv~3y"+4y"+2y-4y=sin(x) Приступим к поиску частного решения. В первую очередь нам нужно получить изображение уравнения. Для этого воспользуемся оператором прямого преобразования Фурье iourier (Фурье) панели Symbolic (Символьные). Как н ь случае преобразования Лапласа, все члены уравнения должны быть перенесены в левую часть, которая указывается в левом маркере оператора fouricr. В правом маркере определяется переменная, но которой проводится преосфазова1те. 4.2i4B-fouriei(y(x),x,w)-4fouriej(y(x),x,w) + A(a)- l) - -л>д(ю + l) Здесь Д — знаменитая дельта-функция Дирака (она определена для всея х и равна бесконечное тн в одной точке н нулю во всех остальных). Для удобства заменим в последнем выражении переменную fourier(y(x),x,£u) на z, а затем решим полученное уравнение относительно г. 532 ! с.) / • 3 • m / - 4чаг -t-2-itDZ- 4-z + tit-&(a> - l) -tot-A(«i + l) solve,в -* Найдем частное решение уравнения. Для этого применим к решению-изображению обратное преобразование Фурье, задействовав оператор urvfourier панели Symbolic Чтобы результат не был представлен в комплексной форме, воспользуемся оператором complex панели Symbolic. 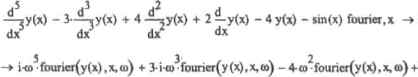 -» 1-я- -д(о) - 1) +а(о + I) i<a + 2-14» - 4 + >i-o - 4.« -Д(ю - 1)ч-д(ш + 1) iп\ fouricr,ш 2 complex 25 -> —sni(t)---cos(t) 25SO ш + 2-i-oo-4 + 3-но - 4м Частное решение найдено. Теперь необходимо найти общее решение однородного уравнения, соответствующего нашему неоднородному: yv-3y",+4y"+2y-Jy—0. Составим для него характеристический многочлен и найдем его корни; 1 5 3 2 roots:=х -3-х + 4-х + 2-х-4salve,х -2 1 + 1 V]~i Из курса высшей математики известно, что общее решение однородного уравнения определяется формулой 1=1 где п — порядок дифференциального уравнения, \ — корни характеристического многочлена (формула справедлива для случая отсутствия кратных корней). Имея вектор корней характеристического уравнения, несложно написать программку, которая представляла бы общее решение в таком виде: Gencral solution(poI) ;= а «- О for I • о last(pol) а 4- а + С.-е General solution(roots)C0cK+C1e 2х+С2-е * + Суе(! + ),х + С-е( Избавимся от комплексности вогнете, приведем подобные слагаемые к переопределим константы, чтобы записать общее решение однородного уравнения н стандартной форме. Сп.еЯ+ ClVa-x+ С2.с.ь С3е( + 0Я + С;*0** complex collect, cos(x), sin(x) ,е (С3+ C4)-exco8(x)+i(C3-C4).et-sin(x) ♦ Св+С,-* * + fye i.(G3-C4) = k2 c3 + c4=ki kl-ex-cos(x) + k2exsin(x) + CQ-eX+Cj-e 2x+CjX * Чтобы получить конечный результат —общее решение неоднородного уравнения, прибавим к общему решению однородного уравнения частное решение иеодтгородкого. 3tэсх — . \ х 2J SolutionskJc cos(x) + k2-c sin(x)+C.-e +C,e + C„-e---sin(x)---cos(x] 0 12 2550 Проверка показывает, что найденный нами отпет абсолютно верен: substitute, у(х) = Solution 532 --=у(х)-3--.у(х)+4-у()1) + 2-у(х)-4у(х)-8т(х) dxdxdxdx simp 11 fy 14.1.3. Интегрирование дифференциальных уравнений С помошью преобразований Лапласа и Фурье можно решать уравнения лишь с постоянными коэффициентами, однако средствами Mathcad можно значительно упростить поиск корней дифференциальных уравнений, коэффициенты которых являются функциями. Как известно, решение любого дифференциального уравнения сводится к интегрированию, которое также выполняется системой очень просто. Пример 14.5. Проинтегрировать дифференциальное уравнение +x)dy + (ху-Jl + х2 sin{x))dx = 0 Преобразуем уравнение в следующую форму: dx х sm(x) 1 + х Обратим внимание на то, что в левой части получено выражение, залакшнэе /. 8 правой части для упрощения выражения стоит разделить числитель ни знаменатель: яsin(x) у>=-. у+ Г--2 •4 1 + х Введем следующие замены: q(x) = 1 + х sin(x) 1 2 Мы получили линейное дифференциалыюо уравнение первого порядка общего вида у+р(х)у-q(x)~0. Из курен высшей математики ипнестпо. что общее решение подобных ypaiiiieinilf ищется в виде p(x)dx р(х) dx У(Х): q(x)e dx+ С 0 ... 139 140 141 142 143 144 145 ... 177 |












