Раздел: Документация
0 ... 142 143 144 145 146 147 148 ... 177 первой производной.)- Такой подход может быть более эффективен в случае не слишком хороню подобранного пользователем шага, а также для решения сложных дифференциальных уравнении С быстро изменяющимися и осциллирующими функциями решений. Если же вам нужно решить жесткую систему уравнений или систему, содержащую нлеебранческис ограничения, следует воспользоваться методом Stiff (рис. 14.6).
Рис. 14.6. Смена и с пользу вмосо численного метода 14.2.2. Решение ОДУ с помощью встроенных функций 13 более старых версиях Mathcad для решения ОДУ использовались специальные встроенные функции. Однако с появлением более наглядного и простого способа, свя-аа иного применением вычислительного блока Given-Odesolve, они уже не представляют особой практической важности. Несмотря на это, о возможности их применения для >ешения одинарного ОДУ нужно иметь четкое представление, так как в некоторых случаях (например, в Нн>граммировании) использовать вычислительный блок нельзя. Гак как для решения одного дифференциального уравнения соответствующие встроенные функции применяются редко, то подробно описывать их в этом разделе мы не будем и сразу приведем соответствующий пример (в случае необходимости читатель бея труда в нем разберется). Обстоятельно же об указанных функциях мы поговорим л разделе, посшпценном решению систем ОДУ. Пример 14.10. Альтернативный метод решения ОДУ (рис, 14.7) у0:=1М:=100 D(t,y) :=8in(i)-y xl:=0х2г=10 yl :=rkfixed(yO,xl,x2,M,D) у2:=Buls!oer(y0.xl,x2,M,D) уЗ :=Rkadapt(y0.xl,x2M,D)
 Рис. 14.7. График решения ОДУ, полученного с помощью встроенной функции г Mixed I (pi[менять приведенные встроенные функции можно лишь для решения дифференциальных уравнений первого порядка, как линейных, так и нелинейных. Найти же с их помощью решение уравнения более высокого порядка, в отличие от использования блока Given-Odesolve, непосредственным образом невоэможио. Впрочем, это можно сделать, сведя указанное уравнение к системе дифференциальных уравнений. Приведем пример решения ОДУ второго порядка с помощью вычислительного блока и встроенной функции rkfixed (реализующей метод Рунге- Кутта четвертого порядка с фиксированным шагом). Пример 14.11. Альтернативные способы решения ОДУ второго порядка (рис. 14.8) Вычислительный блок: Given У(0 +/(t) = 2y(t) у(0)=1у(0>=3 z:=odeso!ve(t,5.100) Сведение к системе ОДУ: DO.y) := 1 r:=rkfixed(yAS,100,D) 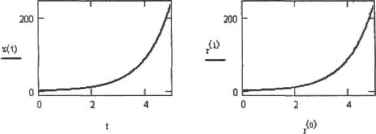 Рис. 14.8. Альтернативные решения ОДУ, полученные с помощью вычислительного блока и встроенной функции Изучив пример 14.11, вы, наверное, согласитесь, что решать дифференциальные уравнения, особенно высокого порядка, гораздо проще п лучше с помощью вычислительного блока, чем встроенных функций. Действительно, зачем выполнять лишнюю, иногда весьма сложную и объемную, работу по разложению уравнения в систему ОДУ, если это отлично может сделать и сама программа. К тому же решение при использовании вычислительного блока получается гораздо более наглядным и доступным пониманию для не владеющего Mathcad человека, чем при применении системных функций с их запутанным синтаксисом. Поэтому, на мой взгляд, прибегать к встроенным функциям для решения ОДУ стоит лишь в том случае, если использовать блок Given-Odesolve невозможно. 14.2.3. Системы ОДУ Начиная с\ \ версии Mathcad возможности вычислительного блока Given-Odesolve значительно расширились, Теперь с его помощью можно находить численные решения не только ОДУ, но и их систем. Как и к ОДУ, к уравнениям системы предъявляются следующие требования: каждое нз них должно быть линейным (высшая производная не должна содержать каких-либо сомножителей) и иметь соответствующее количество начальных или граничных условий. К сожалению, вычислительный блок не может решать системы нелинейных дифференциальных уравнений. Однако в Mathcad имеются специальные встроенные функции, позволяющие находить решен ия как линейных, так и нелинейных систем ОДУ. Всего таких функций три. □Rkfixed(yO,tO,tl,M,D). Задействовав эту системную функцию, можно решить задачу Коши с помощью, пожалуй, самого популярного из численных алгоритмов: метода Рунге-Кутта 4-го порядка с фиксированным шагом. Эта функция подходит для качественного и быстрого решения подавляющего большинства систем ОДУ. □Rkadapt(yO,tQ,tl,M,D). Эта функция реализует адаптивный алгоритм Рунге-Кутта. Ее принципиальным отличием от rkfixed является то, что при вычислении соответствующих приближений она использует не постоянп ый, а зависящий от скорости изменения функций решения шаг дискретизации переменной. Однако, несмотря на это, в качестве ответа Rkadapt возвращает значения функций в равномерно распределенных, исходя нз заданной пользователем величины промежутка, точках интервала. Использовать же рассматриваемую функцию следует в случае более жестких и слож- 0 ... 142 143 144 145 146 147 148 ... 177 |












