Раздел: Документация
0 ... 144 145 146 147 148 149 150 ... 177 Рг :=10 Ь :=- г := 28 3 XDXl-bx2 (5Л D(l,x):= D := rkfixed 6 ,0,50,5000,D 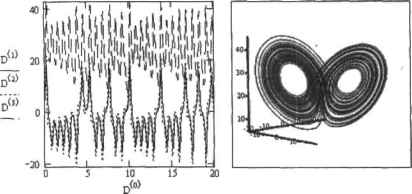 Рис. 14.10. Иллюстрация решения системы Лоренца Пример 14.14. Модель предсказуемого аттрактора Аттракторы — предмет изучения теории хаоса, которая предполагает взаимный переход хаоса и порядка в любой динамической системе. Теория помогает моделировать случайные системы, ко не позволяет предсказать их поведение в будущем. Помимо хаотических, существуют и предсказуемые аттракторы. Например, траектория кназн периодического движения, слагаемого из двух независимых колебаний, в фазовом пространстве может быть представлена как тор. а:=-].5 b:=0.3 В:= I р:=1.2 zf.t) :=B-sin(pt) Y(t,y) - Y:- rkfixed E5* ,500,5000,Y i:=0..5000 f.:=z(0.1f) 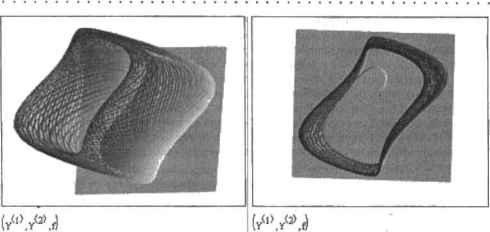 Рис. 14.11. Аттрактор тороидальной формы Время оборота на внутреннем крут тора является частотой одного колебания, два внешнем круге - частотой другого колебания. Примером к во и периодического движения могут служить модуляции колебаний и замкнутом колебательном контуре, состоадемюкатушютшуктивности, конденсатора, сопротивления и источника тока. Принципиальным условием успешного решения системы дифференциальных уравнений я&тяется правильный выбор величины шага (особенно это важно для функции rkfwed). В общем случае для его определения можно использовать то же правило, что и при решении одного уравнения с помощью вычислительного блока (см. лодразд, 14.2.1). Кстати, точность работы функции rkadapt зависит, помимо определенного пользователем количества шагов М. н от значения системной переменной TDL. Более того, меняя ее величину, гораздо проще можно прийти к корректному решению, чем при подборе Количества разбиений интервала В следующем примере мы попробуем оценить степень влияния величины TOL на точность полученного результата. Пример 14.15. Влияние величины TOL на точность адаптивного алгоритма 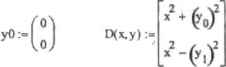 z 1: = RJcadapKyO. 1,2,2, D)22:= Rkadap<yO, 1.2,10000, D) г Ц , = 6.7029358244372448} - 6.703786022251724 TOLr= 10" 16 rl RkadapKyO. 1.2,2. D)z2 := RkadaptfyO, 1,2.10OOO.D) zlj , =6.7037860222954926z2)0000 j = 6.703786022251724 Как можно заключить из приведенного примера, T0L определяет точность результата в конечной точке гораздо значительнее, чем количество шагов. Однако и последний параметр оказывает определенное влияние на качество расчета. Поэтому, решая численно систему ОДУ, подберите эти параметры так, чтобы их изменение в 10 раз не приводило к изменению значений искомых функций в крайней точке (конечно, в пределах интересующих нас десятичных знаков). Стремиться же сделать сразу количество шагав по максимуму большим не стоит: при этом может резко возрасти как погрешность аппроксимации из-за влияния ошибки округления и других факторов, так и время расчетов. Так, использованное в примере 14.15 количество шагов, равное 10 ООО, является неоправданно завышенным, и того же уровня точности можно было достигнуть и при гораздо Меньшем количестве разбиений. В столь же значительной степени, как и функция Rkadapt зависит от TQL и функция Bulstoer. Метод же Рунге-Кутта в стандартной интерпретации, реализуемый функцией rkfixed, в противоположность им находит решение только исходя из длины шага. Для функций, реализующих адаптивный метод н алгоритм Булирща-Штера, в Mathcad существует и другая форма, позволяющая пользователю более значительно влиять на ход поиска решений. Отличается же эта форма от стандартной только набором параметров и тем, что имя соответствующих функций начинается с маленькой литеры (в связи с этим обстоятельством к заданию функций для решения систем ОДУ следует подходить очень внимательно): □rkadapt(yO,x0,xl,acc,0,k,s) - метол Pyrtre—Кутта с переменным шагом: □bulstoer(yO,xO,xl,acc,D,k,s) - метод Булирша-Штера. Наборнараметровдляпривсде111!Ыхфу111ЩИЙ11детичеп и содержит целых семь пунктов: □уО — вектор начальных условий. Задается точно так же, как для рассматриваемых функций в стандартной интерпретации; □хО — начальная точка интервала изменения переменной: □xl — конечная точка для значений переменной; □асе — погрешность вычисления. Чем меньшим вы определите этот параметр, тем более точным будет результат, однако тем дольше будет вестись расчет. По своим функциям асе полностью аналогичен встроенной переменной T0L в случае использования функций Rkadapt и Bulstoer: □D — вектор-функция, определяющая систему ОДУ; □к — максимальное количество шагов, на которые алгоритм может разбить интервал изменения переменной. Необходимость введения этого параметра связана с тем, что в случае некоторых систем при малых значениях асе количество оборотов цикла алгоритма может быть определено программой столь большим, что времени, которое нужно будет потратить на расчет, потребуется недопустимо много. Кроме того, работать в Mathcad с очень большими матрицами невозможно; □s — минимальная величина шага. Этот параметр необходимо определить в связи с тем, что, в частности, при слишком малой величине шага погрешность разностной аппроксимации может быть весьма значительна. Использование приведенных функций имеет ряд особенностей. 1. Вы заранее не можете определить, в скольких точках Mathcad вычислит решение вашей системы. Вы можете лишь задать верхнюю границу их количества. А это может быть не всегда удобно — например, при не слишком высоком уровне точности асе решение может быть получено но столь малому количеству разбиений, что по- 0 ... 144 145 146 147 148 149 150 ... 177 |












