Раздел: Документация
0 ... 141 142 143 144 145 146 147 ... 177 ке используются те же правила, что и при задании выражения самого дифференциального уравнения. □ Когда ОДУ, начальные или граничные условия будут заданы, можно непосредственно приступать к вычислению значений искомой функции на нужном промежутке. Для этого следует задействовать специальную функцию odeso!ve([vector],t,b,[step]), где: •vector — вектор функций, относительно которых решается система дифференциальных уравнений. Вектор должен содержать имена функций без имени переменной. Данный параметр используется, когда ны решаете систему ОДУ, в случае же решения одиночного уравнения его следует опустить; •t — переменная, от которой зависит искомая функция. Необходимость задания этого параметра связана с тем, что, как это ни покажется странным, результат использования функции odesolve также является функцией, а не вектором некоторых числовых значений. Те возможности, которые открывает это обстоятельство, мы продемонстрируем немного ниже; •b — правая граница интервала поиска решения. Соответственно левая граница определяется вами при задании начальных условий. Обязательным условием является то, что b должно лежать правее а - это общее требование для корректно заданной задачи Коши при использовании всех численных методов; •step - этот параметр определяет количество шагов, используемых численным методом Рунте-Кутта. Задание step не является обязательным, и по умолчанию этот параметр определяется таким образом, чтобы длина шага была равна 0,!. В случае сложных уравнений правильное определение step может играть самую принципиальную роль для получения корректного решения. Однако стремиться во всех случаях сделать step минимальным не стоит, так как для большинства ОДУ это приведет лишь к резкому увеличению времени расчетов без значимого повышения их точности. Наряду с дифференциальными уравнениями в блоке Given-Odesolve можно задавать и алгебраические ограничения, например, y(t)+z(t)-=w(t), что позволяет ввести В систему дополнительную неизвестную функцию w(t), которая должна быть определена odesolve наряду с y(t) и z(t). Ограничения же в виде неравенств задавать нельзя. Приведем пример решения ОДУ первого порядка. Выберем уравнение таким образом, чтобы оно было не решаемо аналитическими методами (следует заметить, что всевозможными символьными преобразованиями можно привести к удобному для интегрирования виду предельно ограниченную группу дифференциальных уравнений). Пример 14,7, Численное решение ОДУ первого порядка (рис. 14.3) Given У(0) = 1 у :=odesolve(t,40) у(6.1 П15) - 2.5930254520046692 у(39.89679) = 6.6616193367807526 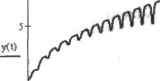 -I-г за40 i Рис. 14.3. График численного решения ОДУ первого порядка Обратите внимание, что прн решсттии дифференциального утонения с помощью функции odesolve существует возможность определения значений искомой функции и в тех точках, которые не являются узловыми (то есть нетто средстве шю в ходе работы численного алгоритма эти значения просчитаны не были). Достигается же это за счет задания между каждой парой точек интерполирующего полинома (точнее, кубического сплайна). Очевидно, что точность такого предсказания будет тем выше, чем меньше величина шага и чем более плавно и предсказуемо изменяется функция решения. Кстати, и график решения ОДУ вычислительным блоком Given-Odesolve задается таким образом, как будто оно является непрерывной функцией (см. рнс. 14.3). Аналогичным образом, как и ОДУ первого порядка, решатотся в Mathcad и линейные дифференциальные уравнения, содержащие производные более высокого порядка. Пример 14.8. Решение ОДУ третьего порядка (рис. 14.4) Given yO + yO + yW + yd-t-sinO) У"(0)-2 у(0)=1 У(0)=0 у :=odeaolve(t,30,30000) 200т  I Рис. 14.4. Модель резонирующей колебательной системы Изучая пример 14.8, вы, наверное, заметили, что дифференциальное уравнение в нем задано иначе, чем в примере 14.7. Вообще же, обе зги формы абсолютно эквивалентны, и выбор одной из них должен определяться прежде веет вашими предпочтениями и той областью, к которой относится решаемое уравнение. Важным условием успеха при численном решении дифференциальных уравнений является правильный выбор величины шага. Так, если он будет определен недостаточно малым, то найденное решение может быть весьма и весьма далеким от истинного. Приведем пример ошибочного решения ОДУ при слишком большой ширине шага. Пример 14.9. Осцилляция при недостаточно малой длине шага (рис. 14.5) Given у(5) = 5 у := odesolve(l,50,10)у 1 := odesolve(t,50,1000)" МО1 т 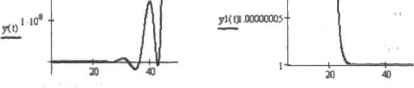 t t Рис. 14.5. Ошибочное (слева) и верное (справа) решение дифференциального уравнения Конечно, в приведенном примере возникшая ошибка (см. рис. 14.5) связана с иску ест венно завышенной длиной шага, и даже при использовании его величины, принятой по умолчанию (step-0.1), решение было бы найдено верно. На практике бывает необходимо решать такие дифференциальные уравнения, нужное значение шага для которых может быть совсем не очевидно (и step-0.1 для них будет порождать еще более значительные колебания или отклонения, чем step-4.5 в примере 14.9). В тех случаях, когда у вас возникают сомнения в верности заданной вами длине шага, вы можете руководствоваться следующим простым правилом: ее можно принять как корректаую, если уменьшение ее велячИ1ГЫ в 10 раз не приводит к изменению результата в некоторой точке в пределах количества десятичных знаков, отвечающего нужному уровню точности. Как уже было отмечено выше, по умолчанию вычислительный блок Given-Odesoive использует популярный метод Рунге-Кутта 4-го порядка с постоянным шагом. Однако Mathcad позволяет сменить его при необходимости на так называемый адаптивный алгоритм (adaptive) или алгоритм решения жестких систем (stiff). Чтобы это сделать, щелкните правой кнопкой мыши на функции odesolve. В открывшемся при атом контекстном меню переместите флажок из строки Fixed (Фиксированный) в строку Adaptive (Адаптивный) или Stiff (Жесткий). Отличие адаптивного метода <я простого алгоритма Рунге—Кутта состоит в том, что используемая им длина шага не постоянна, а зависит от скорости изменения функции результата (что определяется, в частности, величиной 0 ... 141 142 143 144 145 146 147 ... 177 |












