Раздел: Документация
0 ... 140 141 142 143 144 145 146 ... 177 Приступим к непосредственному решению уравнения. Подставим в формулу выражения для р(0 и q(x): (с* -dx у(х) :=с sin(x) £7i dx l+x* dx+ С Символьно вычисляем корни уравнения. Геометрически они представляют собой семейство интегральных кривых зависящее от параметра С: У(х) I • ("cos (x) + С) Решение однородных уравнений первого порядка сводится к замене переменных, превращающих их в уравнения с разделяющимися переменными. Последние удается проинтегрировать в Mathcad так же легко, как, в частности, и уравнения а полных дифференциалах. Пример 14.6. Проинтегрировать дифференциальное уравнение xdy - (l - V*) dx "0. Построить интегральную кривую, проходящую через точку М( 1; 7/3) 8 два действия данное уравнение приводится к виду dy =-dx х Проинтегрировав обе части, мы найдем общее решение, оп5сдоляющео однопараметричвеков семейство интегральных кривых: у(») dx ) 22 2 у(х) 1й(х) -6-х + 3 • х - - х I 3 2 2 у(х) - 1п(х) - б х + Зх~-х+С Чтобы кийтн требуемое частное решение, необходимо определить фиксированное значение параметра С. Для этого подставим в последнее выражение координаты точки М, а затем разрешим полученное уравнение относительно С: --ta(l)+** I2-3+ -I2-Csorve.C -> 6 33 Записываем функцию решения с численным значением параметра С: 1I 22 2 у(х):« bfx) - 6 х +3-Х---Х +б Строим интегральную кривую (рис 1-1.2) 10 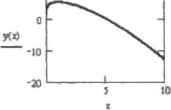 Рис. 14.2. Интегральная кривая решения, проходящая через точку М(1; 7/3) 14.2. Численное решение ОДУ в форме задачи Коши Основная форма задания исходных условии, которая используется при моделировании реальных процессов с помощью дифференциальных уравнений, связана с определением значений всех низших производных в начальной точке шггервала изменения перемен но ft. Так, в физике ОДУ обычно описывают изменение изучаемой характеристики с течением времени, и начальные условия определяются в момент t-О. Заданные таким образом дифференциальные уравнения и системы дифференциальных уравнений называются задачами Коши. Методы численного решения ОДУ в форме задачи Коши разработаны весьма досконально. Самыми популярными из них заслуженно являются алгоритмы Рунге-Кутта, успешно используемые для решения подавляющего большинства дифференциальных уравнений. Однако для некоторых задач (например, жестких систем химической кинетики) они неприменимы (илн неэффективны), и тогда приходится применять более тонкие и сложные методы. Функции, реализующие наиболее важные иа них. являются в Mathcad системными, что позволяет очень быстро и просто находить решение практически для любого ОДУ или системы ОДУ. Решение .тинеЙ1(ыхдифференциа1ЬНЫхуравнешй и их систем реализовано в Mathcad н двух формах: в виде вычислительного блока и в виде встроенных функций. Первая форма предпочтительнее с точки зрения наглядности представления решения н технической простоты, вторая же открывает куда более широкие возможности для влияния на ход сто получения и изучения полученных результатов. Так как. вне зависимости ш выбора типа оформления, система использует для решения ОДУ одни и те же алгоритмы, то принципиального различия оттого, какой из них вы предпочтете, в результатах вычислений не будет. Далее мы обсудим принципы решения ОДУ п систем ОДУ, заданных в форме задачи Коши обоими альтернативными методами, а Также отдельно поговорим о жестких задачах. 14.2.1. Вычислительный блок Given-Odesolve С такой формой проведения расчетов, как вычислительный блок (So)ve Block), мы уже Мтречялмсъ, когда разбирали методы численного решения алгебраических уравнений (функция find), минимизации невязки системы (функция minefr). а также определения зкетремумов (функции Maximize и Minimize). Самый простой и наглядный способ численного решения линейных ОДУ н систем линейных ОДУ в Mathcad также использует вычислительный блок. Чтобы его реализовать, выполните следующую последова-гельность действий, □Залайте вводное слово Given (Дано). □Ниже вводного слова определите вид дифференциального уравнения или системы уравнений. Сделать это нужно, соблюдая следующие правила. •Дифференциальное уравнение (в том числе входящее в систему) должно быть строго линейным (то есть высшая производная в нем не должна иметь никаких сомножителей или степенных показателей). Подобное ограничение связано с особенностями используемого (по умолчанию) системой при решении ОДУ н форме вычислительного блока Given-Odesolve метода Рунге-Кутта4-го порядка точности (о нем мы поговорим ниже). Если же ваше уравнение нелинейное, то использовать вычислительный блок нельзя. > Производные а выражении дифференциального уравнения могут быть заданы с помошью специальных операторов панели Calculus (Вычисления) (Shift*/ для оператора производной первого порядка и Shift+Ctrt+/ для оператора дифференцирования произвольного порядка). Подобная запись дифференциальных уравнений более принята в физике, а в математике традиционно производные в ОДУ обозначаются с помощью специальных меток-штрихов. При задании вычислительного блока можно использовать и такую форму отображения дифференциальных уравнений (соответствуюц1ИЙ штрих вводится с помощью сочетания Ctrl+F7). •Искомые функции должны быть определены явно с указанием имени переменной, например f(x). •В качестве знака равенства внутри вычислительного блока следует использовать, как н в случае решения простых алгебраических уравнений, только логическое равенство (Bold Equal - Ctrl*-). * □Помимо самого дифференциального уравнения, внутри вычислительного блока необходимо задать п соответствующие начальные или граничные (в случае решении краевых задач) услоиия. В курсе высшей математики доказывается, что для того, чтобы получить явное решение ОДУ п-го порядка, для него следует определить п начальных условий. В случае задачи Коши в качестве начальных условий необходимо задать значения производных порядков п-1,п-2,...,0 на левой границе интервала изменения переменной. При определении производных в начальнойточ- 0 ... 140 141 142 143 144 145 146 ... 177 |












