Раздел: Документация
0 ... 145 146 147 148 149 150 151 ... 177 строить иа основании его гладкий график можно будет лишь при условии использования специальных функций интерполяции, 2.Очень важным является правильное согласование параметра максимального количества шагов и минимальной их длины. Так, если последний параметр вы определите слишком маленьким, го встроенная функция может не досчитать решения до правой границы заданного интернала в связи с тем, что у нее просто кончится лимит шагов. 3.Поскольку длина шага в случае использования описываемых функций может различаться для разных фрагментов функций решения системы на порядки, полученный результат далеко не всегда можно использовать для построения кривых или фазового портрета. Для выполнения :ггой работы гораздо лучше использовать функции Rkadapt н В и Ls toe г. 4.Чаще всего рассматриваемые функции используются для получения значения функций решения в конкретной точке (обычно — в конов промежутка). Однако так кап заведомо размерность матрицы решений неизвестна, то для определения количества се строк можно использовать функцию Length(V) (или Last(V)), выделив предварительно с помощью соответствующего матричного оператора один иэ ее столбцов. Приведем пример использования функций rkadapt и bulstoer. Чтобы существовала возможность оценки точности этих функций в зависимости от различных параметров, расчет будем производить для ОДУ второго порядка, решение которого элементарно находится аналитически. Кроме того, в нем мы попытаемся продемонстрировать все изложенные выше трудности при применении рассматриваемых функций. Пример 14.16. Функции rkadapt и bulstoer Решаемое уравнение второго порядка с начальными условиями: у"(х) + 10у*(х)-х+ 10у(х)= О уЩ = О Его точное аналитическое решение: У(0) = 1 5х* у(х) :=е Преобразование ОДУ второго порядка п систему ОДУ в векторной форме (переносим в правую часть уравнения все слагаемые, кроме содержащего вторую производную, и вводим замены yry(x)./g"7t): ГАХу) 10-(ху1 + у0) Ч пененное решение полученной системы: I уО: t 1 О rl :=rkadapt0.0,l,10 4,D, 10Д0.0001) Ы bulstoeryO.0,1,10*4,D, lOO.O.OOOJ) Оценка количества шагпя, потребовавшихся для поиска решения с заданной точностью: last! hi si (ы">) Ы =
Матрицы решений: (0 10 Л 0.01 1-0.1 0.060.982-0.589 0,310,618-1.917 г] = 0.5030.282-1.418 0.7030.084-0.593 0.8290.032-0.267 0.9290.01Э-0.124 I, I 6.711* Ю-3 -0,067J Оценка погрешности всходя из максимального отклонении от аналитического решения: глах(г,(1) -у(г1(0>))= 1.И5-10-4тлал(Ъ/1> v(bi<0>))= 4.365x КГ5 Оценка влиянии па точность решении уменьшения величины асе на три порядка: r2r=rkadapt(y0)0,lft0"T7,D,100v0.000l) Ь2 bulstocr(yO.0,1, Iff 7,D, I00,0.000l) last(r2(l>) = 26lasl) = 5 maxd-y)!), Ю-7 «*ж(ь2(,)-у<Ь2<0))) = 8.803 ,0-9 Оценка значимости правильного согласования параметров: t3:=rkadapt(y0,0,l,10" 15,D,100,o) ЬЗ ;= bulstocr(yO,0,1,10" ,5.D,100,o) 1шч(г30))=99 r398 0 = 0.178 1ш(ьЗ(°) = 1 ] ЬЗ =0.957 (г30> - у(гЗ(0>)) = 2.109 * 10- 14 шах(ьз<1) - у(Ь3(0>)) = 3.015 * 1(Г 14 Решения системы ОДУ, полученные с различной точностью с помощью функций rkadapt и bulstoer, представлены на рис. 14.12. у<=0 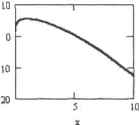 Рис. 14,12. Решения системы ОДУ, полученные с различной точностью с помощью функций rkadapt и bulstoer Изучая приведенный пример, обратите внимание на следующее. □Точность метода Булирша-Штера в случае нашей системы оказалась выше, чем у адаптивного алгоритма Рунге-Кутта при том, что и шагов он использовал меньше, Этот факт можно объяснить тем, что искомые решения являются гладкими и не осциллирующими функциями. При решении же более сложных систем эффективность адаптивного алгоритма может оказаться выше, чем метода Булирша-Штера, □Чтобы найти решение при всех рассмотренных уровнях точности, понадобилось неожиданно мало шагов (особенно это касается функции bulstoer). Учитывая это, не спешите делать количество разбиений при решении ОДУ с помощью стандартных функций большим - для получения результата обычной точности (0.001) для этого бывает вполне достаточно всего несколько десятков шагов. □Если вы хотите построить график решений системы ОДУ, сделайте величину асе поменьше (10"*-] О"1). В этом случае система сгенерирует достаточно точек для задания гладкой кривой. При обычной же точности по полученным данным вы сможете построить лишь весьма грубую ломаную. □Очень важно правильно согласовать параметры точности, максимального количества шагов и минимальной их длины. Так, в приведенном примере при асс-Юн отсутствии ограничений на размер шага адаптивный алгоритм смог просчитать функции решения только на 1/10 длины интервала (см. правый график рисунка из примера 14.16), Для того же, чтобы получить с помощью него корректное решение, лимит количества шагов должен быть увеличен до 2000. Зато при том же наборе парзмет-ров функция bulstoer нашла результат всего при 11 разбиениях — более чем в 100 раз меньшем их количестве, чем понадобилось rkadapt Этот факт как нельзя лучше демонстрирует, как сильно определяет успех расчетов правильный выбор алгоритма. Чтобы проиллюстрировать, как различается шаг на промежутке при адаптивном его определении, построим, исходя из полученных а примере 14.16 значений, диаграмму (рис, 14.13), i := 0.. lBrt(t2(1>)j := 0.. Iast(b2) -1- О О О О О О—в—О С 4 .....□....................;л 1 D0JI Рис. 14.13. Переменный шаг использованный функциями rkadapl и bulstoer Из приведенной диаграммы следует, что шаг, используемый численными методами, зависит ках от скорости изменения функций системы, так н от их величин. Чтобы продемонстрировать все возможности Mathcad в решении систем ОДУ, рассмотрим на примере нахождения траектории ракеты, насколько эффективно справляется с поставленной задачей вычислител ьныЙ блок Given-Odesotve. 03 0 ... 145 146 147 148 149 150 151 ... 177 |












