Раздел: Документация
0 ... 148 149 150 151 152 153 154 ... 177 на промежутке [tetj методом Симпсона, о котором мы говорили ранее. Функция в этом случае интерполируется параболой. Чтобы определить ее вид, достаточно трех точек подынтервала, в которых значение функции известно. Выше мы определили четыре таких точки: k1, k2, кЗ и к4, поэтому в середине промежутка наклон кривой зададим как среднее арифметическое к2 и кЗ, Применив формулу Симпсона с половинными шагом, мы найдем приращение искомой функции иа данном подынтервале. Эта идея лежит в основе метода Рунге-Кутга4-го порядка, который позволяет подобным образом рассчитать приращение функции на всем интервале [tJ. Исходя из условия y(t(,)~yO, мы нашли решение у, в точке tr Аналогично, приняв за начальное условие ytt-y,, можно определить функцию в точке tin и т. д. В общем виде Чтобы наглядно представить всю последовательность действий, проведенных нами выше, напишем программу, реализующую данный метод. Пример 14.18. Программная реализация метода Рунге-Кутта 4-го порядка (рис. 14.19) kl + 4- (k2+ ЬЗ) 2 + к4 + -(к1 + 2к2+2кЗ + к4) for isC.M kl <- f(t,y.) 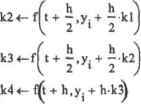 (kl + 2-k2+ 2кЗ+ к 4) 6 if i 5 M - 1 С №ГМ((Г,0.10,1.100) 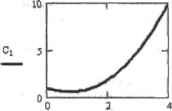 Рис. 14.19. Решение ОДУ с помощью приведен кого алгоритма В корректности работы программы легко убедиться, сравнив решения, полученные с помощью встроенных функций и нашего алгоритма. 14а каждом шаге алгоритм алпрокс и миру ет дифференциал ьное уравне юге по приведенной схеме, поэтому попытаемся проанализировать, какие факторы влияют на точность полученных с его помощью результатов. Очевидно, возникает ошибка приближения искомой функции параболой при использовании формулы Симнсона, а также погрешность усреднения значений к2 и кЗ в центральной точке подынтервала. Такой подход к оценке погрешности можно назвать геометрическим. С аналитической точки зрения метод Рун-ге-Кугта 4-го порядка использует для нахождения решения только первые пять слагаемых, полученных при разложении искомой функции в ряд Тейлора в окрестности заданной точки. Если на отдельном шаге погрешность пренебрежимо мала, то на интервале происходит накопление ошибки, что отражается на точности результата. Поэтому важно выбрать оптимальное соотношение между длиной шага и их количеством, при котором погрешность аппроксимации окажется минимальной, а время расчета приемлемым Как правило, с уменьшением длины шага точность возрастает до определенной величины, которая не меняется при дальнейшем разбиении интервала. Проиллюстрируем сказанное. В табл. 141 приведены истинные решения задачи Коши у{1)~7-у, у(0)-1 на интервале [0:10], а также рассчитанные нашим алгоритмом при различной длине шага. Таблица 14.1. Решения задачи Коши y"(t)=i3-y, y(0)=i на интервале [0; Ю] методом Рунге-Кутта 4-го порядка
Как нидио иэ таблицы, при длине шага, равной 0.1 (используемой системой по умолчанию), решения оказываются точными до четвертого знака. Уменьшение длины шага до 0.01 увеличивает точность до седьмого знака. К сожалению, подобная закономерность реализуется далеко не для всех функций. Выбор желаемого уровня точности остается за пользователем, но зачастую оценить величину ошибки при той или иной длине шага просто невозможно. В атом случае альтернативным оказывается метод Рунге-Кутта с переменным шагом (адаптивный метод), лежащий в основе работы функций rkadapt и Rkadapt В каждой узловой точке интервала этот алгоритм находит два варианта решения, используя схемы Рунге-Кутта 4-го и 5-го порядков. Если разность между полученными значениями оказывается меньше допустимой величины ошибки (которую можно заранее задать через системную переменную T0L), то длина шага увеличивается. Если же разность превысит ошибку, то следующую точку интервала алгоритм определит с меньшей длиной шага. В случае равенства обоих параметров шаг остается постоянным. Адаптивный метод целесообразно использовать для нахождения неоднородных решений, меняющихся с различной скоростью на том илн ином участке интервала. Это позволит сократить время расчета, поскольку для некоторых функций хороший результат может быть получен и при использовании алгоритмом небольшого количества шагов. Метод Булирша-Штера Алгоритм Булирша-Штера (Bulirsch-Sloer), реализованный во встроенных функциях bulstoer и Bulstoer, дает хорошие результаты для гладких функций решения. В его основе лежит численное приближение решения на промежутке х;х+Н методом рациональной экстраполяции. Серия значений, полученных на интервале интегрирования, экстраполируется в конечной точке интервала к истинному решению полиномом, приближающим функцию (рис. 14.20). 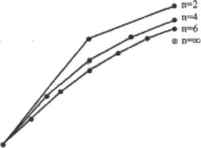 -1—а* жк+Н Рис. 14,20. Иллюстрация метода Булирша-Штерв Приближение оказывается тем точнее, чем больше шагов было выбрано внутри интервала. Понятно, что при стремлении их количества к бесконечности оно превращается в точное аналитическое решение, ио при этом неограниченно возрастает и время расчета. Сократить его можно, задав требуемую точность решения TTJL через параметр асе. 0 ... 148 149 150 151 152 153 154 ... 177 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












