Раздел: Документация
0 ... 150 151 152 153 154 155 156 ... 177 протекает с определенной скоростью, которая характеризуется константой скорости kn Схематично все процессы можно представить следующим образом: E + S ~к2 ES кЗ Р + Е Под скоростью реакции понимается изменение (уменьшение) концентрации реагирующих веществ в единицу времени. Чем больше kn, тем соответственно больше и скорость реакции. Кроме того, нетрудно догадаться, что реакция будет протекать тем быстрее, чем больше концентрация исходных компонентов, Учитывая эти факты,запишем уравнения, описывающие изменение концентрации веществ в реакционной системе стечением времени. Концентрация исходного реагента S уменьшается но мере образования про межуточного комплекса ES и восполняется за счет его частичного распада: ) = -kl-[E]-[S]+k2tES] ш Концентрация фермента Е уменьшается но мере образования промежуточного комплекса ES. Противоположный процесс наблюдается при регенерации фермента Е в результате образования продукта Р, а также при разрушении комплекса ES: ЙЕ! =-kl-EB] [S] + (k2 + k3)[ES] dl Концентрация промежуточного комплекса ES увеличивается за счет связывания фер-Meina Е с веществом S. При образовании конечного продукта Р и при разрушении комплекса концентрация ES в реакционной системе падает. S = kI-[E]-[S]-(k2+k3)[ES] dt Конечный продукт Р накапливается в системе за счет распада комплекса ES: dt Итак, мы получили систему уравнений, решение которой представлено в примере 14 20 Чтобы получить задачу Коши, в систему необходимо добавить начальные условия -исходные концентрации фермента Е и вещества S. Разумеется, в момент начала реакции концентрации промежуточного комплекса ES н продукта Р будут равны нулю. Изучая пример, обратите особое внимание на особенности задания параметра J. Пример 14.20. Решение жесткой системы ОДУ с помощью встроенных функций у0:= kl:= 10" r 1 1 0.1 о о; к2:= 10 FCt.y) ;= кЗ:=10~ 3 -ki-JTj -у2 + к2у0 -к1угу2 + (к2+ кЗ)у0 kl-y( у2 -(к2+кЗ)у0 ill dx dx X ipi dx 7F(t-y)i 7*1 ** dt 1 dx 1 L K*4 V1 о 7*k 114 dx L Vy3/ dx V1 if(t,y)2 -ju dtdx 1 уз/ f X V dx l v ч У -1 /. dx yo 1 in dx -0 \ y2 L Vy3/ (0 100 -1000000-У, L fv Yl 2 !Н dx dx y3 J 7 dx J(.y) L \ *JJ -1000000У, 0 » Jf» -,000000- -1000000-У, 0 1000000 y, 0 I /0 1000 100 -1000000-У, -1000000 y, 0\ 0 ism -."ооовл -1000000-У, 0 юооооо-yj 0 0 I 1000 si Stirrb(yO,0,1000,5000, F,J) 00 <Stiffi<yO, 0,1000.5000, F.J) Полученное нами решение абсолютно адекватно физически (рис. 14.23): с течением времени концентрация исходного вещества S падает (sl<l>) по мере накопления в реакционной системе конечного продукта Р (sl<4>). На начальном этапе, когда количество Е и S в системе велико, происходит нх интенсивное взаимодействие, вследствие чего концентрация комплекса ES резко возрастает. Затем за счет образования продукта P н частичного разрушения комплекса концентрация ES постепеино снижается (sl<3>). Процесс превращения S в Р протекает с участием фермента Е с последующей его регенерацией, поэтому концентрация Е в ходе реакции практически не меняется 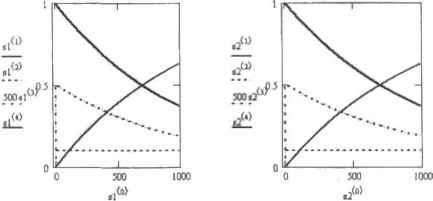 Рис. 14.23. Решение жесткой системы дифференциальных уравнений Обратите внимание, каким интересным н необычным способом был подсчитан нами якобиан. Мы использовали ту особенность решаемой системы, что в ней нет никаких специальных функций, и все искомые элементы входят в нее в первой степени. Л это означает, что при вычислении п]юизводной по определенной неизвестной, последняя будет исключена из уравнения. Поэтому, не сделан никакой фактической ошибки, мы просто заменили соответствующие элементы вектора у на переменную х. Необходимость этой операции связана с тем. что оператор дифференцирования Mathcad не может вычислять производной по матричному элементу. Безусловно, вы можете сказать, что приведенный п рассматриваемом примере способ задания якобиана чрезмерно громоздок н гораздо легче было бы просто подсчитать его элементы в голове, Конечно, в случае таких простых для вычисления производных функций, какими являются правые части уравнений химической кинетики, следует поступить именно так. Однако для более сложных систем представленный способ аналитического вычисления якобиана является наиболее простым в реализации среди всех возможных в Mathcad. Поэтому его стоит запомнить. Продолжая разговор о якобиане, поясним, для чет он нужен встроенным функциям группы Stiff. Все дело в том, что в теории численных методов доказано, что чем более вырожденным является якобиан системы ОДУ, тем она более жесткая. То есть матрица Якоби является относительной мерой жесткости, и это ее свойство может быть использовано для наиболее оптимальной настройки численного метода. Когда определитель якобиана, вне зависимости от значений функций и переменной, равен нулю, система имеет предельно высокую степень жесткости. 0 ... 150 151 152 153 154 155 156 ... 177 |












