Раздел: Документация

0 ... 149 150 151 152 153 154 155 ... 177

На промежутке последовате-ч ьно выбираются п-2,4,6,8.10 и т. д. шагов ннтегтжрова-ни» с постоянно уменьшающейся длиной до тех пор, пока разность между полученными на конце интервала значениями не окажется равной T0L. Последний результат заносится в матрицу решений, выбирается следующий промежуток, и все операции повторяются заново. Проанализируем консрегнь1Й пример, чтобы оценить, каким образом влияют па точность решения выбранное алгоритмом количество шагов и величина T0L

Пример 14.19. Влияние количества шагов и величины TOL на точность алгоритма Булирша-Штера

Sys(t.y):

2-У

уО

x:=bulstoer(yO,0,10,10 \ Sys , 10,0. l) Xj j =932674444016026

x:= bulstoerO.O.lO.lO-3, Sys,10O00, 0.1 *5 ] = 9.32674444016026

у := Ьшяоег(у0,0,10,I0~ 6,Sys, lO.O.l) 9.99770030614651

m

5,1

)

y:= bulstoerO.0,

10,10 Sy*,lOOOO.O.l)

y5i, = 9.99770030614651

35

50

Как видно, точность решения, полученного методом Булирша-Штера, зависит не от количества разбиений всего интервала поиска, а от заданной величины TOL, которая определяет внутреннее количество шагов каждого Промежутка [х;х+ Н].

14.2.5. Жесткие системы ОДУ

Понятие о жесткости (Stiff) системы дифререцдиальных уравнений появилось в сере дине XX века в связи с решением систем, описывающих протекание катализируемых химических реакций. Оказалось, что такие, казалось бы, эффективные и абсолютно надежные численные методы, как алгоритм Рунге-Кутта (да и нее другие разработанные на том этапе явные алгоритмы) не способны решать системы подобного рода. Это неприятное открытие послужило толчком для развития обширнейшего и важнейшего направления в математике числе и пых методов, и сейчас алгоритмы, способные решап. жесткие системы, играют па практике куда больигую роль, чем классические явные методы.

Точного определения жесткой системы ОДУ и общем не су Шест ну ст. Обычно жесткой считается система, описывающая сильна разномасштабные процессы. Трудности, связанные с решением таких систем явными численными методами, объясняются тем, что условие устойчивости требует брать шаг слишком мелким. А это означает, что для того, чтобы найти корректный результат, алгоритм придется про1срутнть миллионы или даже миллиарды раз, что может быть непосильной задачей даже для современного компьютера.

---

Рассмотрим следующее простейшее линейное ОДУ:

-y(0 = -a-y<t) dt

При небольшом значении коэффициента а вычислительный блок Given-Odesolve (реализующий метод Рунге-Кутта 4-го порядка с фиксированным шагом) без проблем решает это уравнение (рис. 14.21). Например:

Given

-У(0 = ~ау(0 У(0) = 1 f:=Odesolve(i,3,10)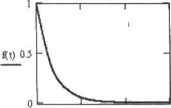

D1JЭ

t

Рис. 14.21. Верное решение ОДУ

При увеличении же значения коэффициента а до 30 в решении появляется неустойчивость (рис. 14.22).

1-1-р

0133

t

Рис. 14.22. Неустойчивость численного решения ОДУ

Приведенный пример показывает, что одни и те же уравнение или система уравнений могут быть жесткими или нет в зависимости от значения (точнее, соотношения) входящих в них параметров. Как правило, чем более различаются коэффициенты при разных членах уравнений системы ОДУ. тем более сложно решить ее с помощью обычных численных методов. Это связано с тем, что чем жестче система или уравнение, тем больше требуется шагов для устойчивой работы численного алгоритма. Так, например,

---

14.2. Численное решение ОДУ в форме задачи Коши .; 471

I » t 1 > • i > t1* t Н i i < 1 t i Hit if > i i « t i t i i t t • « t « i t i i i <

чтобы подучить верный результат для рассматриваемого уравнения при а=30, следует разбить промежуток не на 10, а на 50 отрезков. Однако в случае многих жестких систем невозможно прийти к верному решению обычным уменьшением длины шага, поскольку такой подход потребует столь огромного количества оборотов цикла, что задача будет не решаема в вычислительном плане.

Разрешена же данная проблема была с помощью так называемых неявных абсолютно устойчивых разностных методов. Особенностью этих методов является то, что они устойчивы при любой величине шага, поэтому последний может определяться только исходя из соображений точности. В Mathcad жесткие системы ОДУ можно решать двумя способами: с помощью вычислительного блока Given-Odesolve, выбрав в контекстном меню функции Odesolve неявный алгоритм Stiff, либо задействовав встроенные функции, реализующие наиболее популярные неявные методы.

□Stiffb{yO,tO,tl,M,F). Метод Булирша-Штера для жестких систем ОДУ;

□Stiffr(yO,tO,tl,M,FJ). Метод Розенброка для решения жестких систем ОДУ;

□Radau(y0, t0, tl, М, F). Метод RADAU5 (в терминологии справочной системы Mathcad) для жестких систем ОДУ,

Данные функции требуют задания следующих параметров:

□уО — вектор начальных условий. Задается точно так же, как при решении простых систем ОДУ;

□t0— начальная точка для переменной;

□Н — правая граница для интервала изменения переменной;

□М — количество шагов, которое должен использовать численпый метод;

□F — векторная функция, определяющая систему ОДУ. Задается точно по таким же правилам, как и в случае использования функций решения нежестких систем;

□J — матричная функция размерности NrfN+1), гдеЫ — количество уравнений в системе. В первом столбце 0 должны находиться функции производных соответствующих строк F по независимой переменной. В остальных N столбцах должен быть расположен якобиан (матрица частных производных всех соответствующих уравнениям функций по всем входящим в них переменным) решаемой системы дифференциальных уравнений. Аналогично F, J должна быть задана как функция двух переменных.

Результатом работы перечисленных функций, как и всех остальных встроенных функций, предназначенных для решения систем ОДУ, является матрица, в первом столбце которой содержатся значения переменной, а в остальных — соответствующие нм величины искомых функций.

Обратите внимание, что функция Radau не требует задания якобиана, однако при се использовании необходимо повысить точность вычислений, уменьшив значение встроенной константы T0L Точность расчета с помощью Stiffr и Sriffb также определяется 70L

Рассмотрим решение жесткой системы ОДУ на примере задачи химической кинетики. Пусть исходное вещество S под действием фермента Е превращается в конечный продукт Р. Фермент Е, действуя на вещество S, образует с ним промежуточный комплекс ES. после распада которого происходит образование продукта реакции Р и регенерация фермента Е. Комплекс ES не является абсолютно устойчивым и может разрушаться с образованием исходных реагентов. Каждая из перечисленных стадий реакции

0 ... 149 150 151 152 153 154 155 ... 177