Раздел: Документация
0 ... 151 152 153 154 155 156 157 ... 177 Интересно, что в решении этой же системы, полученном с помощью вычислительного блока Given-Odesotve (методом Stiff) наблюдается осцилляция (рис. 14.24), указывающая на неустойчивость алгоритма, а при попытке решить систему с помощью функции Radau решение вовсе расходится. 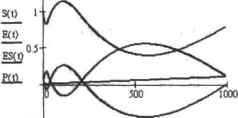 I Рис, 14.24, Осцилляция решения жесткой системы ОДУ, полученного с помощью вычислительного блока Given-Odesolve Возникшие проблемы связаны в первую очередь с тем, что оба метода не требуют задания якобиана в символьном виде, что, безусловно, снижает эффективность их работы. Используя блок Given-Odesolve к функцию Radau, можно быстро получить решение менее жестких систем, не тратя время на составление громоздкого якобиана. Однако найти решение особо жестких систем с их помощью не удастся, в таких случаях нужно пользоваться функциями семейства Stiff. Следует помнить, что для корректной работы функций Stiffb н StiffY также необходим тщательный подбор входных условий. Так, снижение начальной концентрации фермента Е в рассмотренном примере с 0,1 до 0,01 увеличивает жесткость системы, и ее решение оказывается непосильным даже для Stiffb я Stiff г при любом количестве шагов. Аналогично функциям для решения простых систем ОДУ, для встроенных функций Stiffr и Stiffb имеются модификации, позволяющие определять решение а одной (конечной) точке (например, в задачах химической кинетики интерес представляют концентрации реагентов именно в определенный момент времени): □5tiffr(yO,tO,tl,acoFJ,k,s) — метод Розенброка; □Stiffb(y0,t0,tl,acc,FJ,lc5) - метод Булирша-Штера; □radau(yO,tt), tl, асе, FAs)-метод RADAU5. Данные функции имеют весьма значительное количество параметров - восемь, что, однако, позволяет пользователю активно влиять на ход поиска решения. Особенности определения параметров в случае применения функций stiffb н stiffr точно такие же, как при использовании функций bulstoer и rkadapt, поэтому подробно останавливаться на них мы не будем. Единственное же отличие состоит в том, что вам необходимо задать, в связи со спецификой алгоритмов для решения жестких ОДУ, функцию якобиана J. что делается точно так же, как для функций семейства stiff в стандартной интерпретации. 14.3. Краевые задачи Красные Задачи отличаются от задач Коши тем, что начальные условия для них задаются на обеих границах интервала поиска решений. В данном разделе мы рассмотрим способы решения краевых задач для ОДУ них систем с помощью встроенных алгоритмов, а также подробно разберем принципы построения разностных схем для краевых задач средствами программирования. 14.3.1. Решение краевых задач для ОДУ с помощью встроенных средств Краевая форма для ОДУ и систем ОДУ используется в основном в физике и технике в Тех случаях, когда определить все начальные значения палевой границе промежутка невозможно. При этом найти решение для заданных таким образом дифференциальных уравнений значительно сложнее, чемдля задач Коши. В Mathcad имеется возможность решения ОДУ и систем ОДУ, заданных в форме краевых задач, с помощью специального численного метода, называемого методом пристрелки или методом стрельбы (shooting method). При этом, аналогично задачам Коши. можно использовать либо вычислительный блок, либо специальные встроенные функции Так как эффективное и с польз она i гне встроенных средств для решения краевых задач требует оггредслениого представления о лежащем в их основе методе стрельбы (shooting method), то нелишне будетрааобратьсявегоприншшах, Прежде всего нужно отметить, что метод стрельбы не предназначен для непосредствен-i юго решен ня дифференциальных уравнений, С его помощью можно лишь преобразовать краевую задачу в форму Коши, определив недостающие на левой границе начальные условия. Сделать же это можно только подбором (естествеино, направленным) 11араметров исходя из того условия, что соответствующие решения полученной задачи Коши о правой крайней точке интервала должны совпадать с исходными краевыми уровнями с определенным уровнем точности. Представим, что нам нужно найти закон, по которому совершает колебания некоторая система, описываемая следующим дифференциальным уравнением второго порядка: -X(t) + X(t) = 0 вЧ Известно, что в начальный момент времени (t.-О) отклонение системы отточки равновесия равно пулю, а амплитудного значения Х=1 оно достигает Ир и t—rt/2. На языке математики эти факты можно выразить следующими краевыми условиями: Х(0) = О Заданное нами выше уравнение является примером двухточечной линейной (тая как при необходимости оно может быть преобразовано в систему на двух линейных ОДУ) нежесткой краевой задачи, и наиболее оптимальный способ ее решения связан с переходом к задаче Коши с помощью метода пристрелки, Реализуя метод стрельбы, прежде всего нужно определиться с недостающим начальным условием па левой границе интервала. В общем случае считается, что это может быть сделано произвольным образом, однако на практике, естественно, можно найти довольно точное приближение за счет тога, что каждый иэ подбираемых параметров имеет вполне реальный физический смысл. Так, например, в машем случае первая производная по X(t) — это мгновенная линейная скорость колебательной системы. Естественно, что хоть ее значение и будет максимальным в момент времени t=0, по величине оно не может быть очень большим (такую оценку можно сделать, сопоставив имеющиеся сведения об амплитудном значении отклонения и периоде колебаний). Учитывая приведенные выше доводы, предположим, что Х(0) равняется, например, трем. Решая заданную таким образом задачу Копти с помощью блока Given-Odesotve, получим функцию решения, [рафик которой приведен на рис. 14.25. 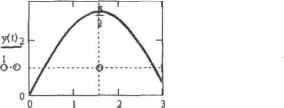 Рис. 14.25. Первое приближение для решения краевой задачи Как видно из графика, функция решения принимает в точке t=7t/2 большее значение, чем оно должно быть исходя из начальных условий. А это означает, что величину се первой производной нужно сделать несколько меньшей, положив, например, Х(0,)-2. Решив при таких значениях начальных условий дифференциальное уравнение, обнаружим, что реально скорость колебательной системы в исходной точке должна быть еще меньше (рис, 14.26), При величине же Х(0)—0\5 окажется, что максимум функции решения лежит ниже заданного изначально уровня. И .тишь определив искомый параметр как 1, находим подходящее приближение. Описанная последовательность действий демонстрирует (конечно, в очень упрощенной форме) основной принцип метода стрельбы. То есть, зная значение функций решения в точке правой границы интервала, очень часто можно, решив последовательность задач Коши (исходя из некоторою начального приближения), найти с определенным уровнем точности и решение самой системы ОДУ. Х(0)=<2Х(0)=О.5Х*(рН 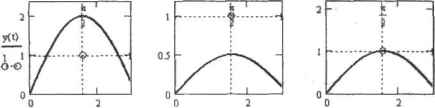 0 ... 151 152 153 154 155 156 157 ... 177 |












