Раздел: Документация
0 ... 154 155 156 157 158 159 160 ... 177 Поскольку решаемое дифференциальное уравнение имеет второй порядок, его нужно преобразовать я снеге «у дифференциальных уравнений первого порядка по описанному В примере 1423 пршщипу. Полученную систему затем задаем в виде вектор-функции D, внутри которой указываем условие изменения массы маятника. к D(t,y) "У 1 m-f.1 + 14(t>4)] + 9,81 Определяем векторные функции начальных условий для обеих грашш временного интервала: loadlCtO.zI) := "Jload2(tl.z2) Задаем условие сшивки: score(if.y) :=у Используя функцию bvalfit, оп>елеляеы недостающие начальные условия: z: = bval fit(z 1, z2, tO, t i, tf, D, load 1. load2, score) 2-(-16.755 6.386) Ha основании полученных данных решаем соответствующие задачи Коши метолом Рунге-Кутта с фиксированным шагом (рис. 14.30): R0:=rk fixed ,0 .0,4,10aD Rl:=rkEUe4 Yl LI loj ,10,4, I0CLD 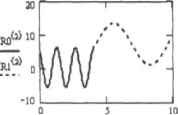 Рис. 14.30. Изменение характера колебаний пружинного маятника с увеличением массы Проанализируем полученное решение. Исходя иа графиха, груз был подвешел к маятнику в момент его максимального отклонения от положения равновесия. Вследствие увеличения массы скорость колебаний уменьшилась, а значит, увеличился их период. Амплитуда колебаний также незначительно возросла, а новое положение равновесия сместилось относительно предыдущего а область более сильных растяжений пружины. Изучив приведенный пример, вы, наверное, согласитесь, чтп, несмотря иа обилие используемых параметров, системы дифференциальных уравнений решаются с помо-. шью функции bvalfit, в обшем, совсем не сложно. Правда, на некоторые момсрггы все же стоит обратить внимание. □Если вы не читали гл. 2, то вам, скорее всего, будет непонятна использованная в правой части дифференциального уравнения запись условия изменения массы: т[1 + 140 > 4)] Все дело в том, что Mathcad умеет анализировать логические выражения и возвращает 0, еслн они ложны, и 1. если их условие оказывается верным. Таким образом, приведенная запись означает, что выражение принимает значение m прн отрицательных t и 15т — прн положите.] ьных. □Приближения для начальных значений должны быть заданы как векторы. Если же, как в нашем случае, на каждой границе имеется только по одному неизвестному параметру, то приближения для них должны быть определены Как первые векторные элементы (но ни в коем случае ие как простые переменные): zIQ:=0г%;-0 □Функция rkfixed, в отличие от вычислительного блока Given-Odesolve, способна находить решения системы ОДУ, даже если граничные значения определены на правой границе интернала. Этот факт был использован нами для построения графика функций решения (особое внимание обратите на последовательность задания параметров): Rita rkfixed Особенности решения краевых задач в Mathcad были изложены нами в этом разделе довольно подробно. К. сожалению, в Mathcad мет встроенной функции, которая реали-joвы вала бы для решении краевых задач одну из многочисленных, созданных для этой цели разностных схем, однако при необходимости вы сможете без проблем задать соответствующий алгоритм и самостоятельно, используя возможности программирования системы. Об зтом мы и поговорим в следующем разделе. 14.3.2. Разностная схема для решения краевых задач К сожалению, далеко не все краевые задачи можно решить методом пристрелки, реализованном во встроенных функциях sbval и bvalfit прн решении уравнений, содержащих быстро растущие или быстро убывающие решения, например е", алгоритм оказывается крайне неточным. Для решения подобных задач существует ряд численных методов, в основе которых лежит построение той или иной разностной схемы. Но в Mathcad нет собственных алгоритмов, позволяющих находить решение конечно-разностным метолом. Однако построить разностную схему совсем не сложно, воспользовавшись программными средствами. Чтобы убедиться в сказанном, рассмотрим принцип метода конечных разностей на конкретном шримере. Решим краевую задачу ЛА ~*(0 - 0.05- —Til) + 5 ХО -sin(0.05- 0 = 0 на интервале (0,20) со следующими граничными условиями: х(0)=0 х(20) = 1 Г/ II н> ,10.4.1040 Для построения разностной схемы на расчетный интервал необходимо нанести сетку линии. В нашем случае уравнение содержит производную но одной переменной, поэтому сетка окажется одномерной. Для уравнений а частных производных, рассмотренных ниже, интервал поиска покрывается двумерной или трехмерной сеткой. Точки пересечения линий пазывахггея узлами, в которых ищутся значения функции. Полученные решения называются сеточными функциями. Понятно, что они не могут быть непрерывными и представляют собой множество, поскольку вычислены при определенных значениях аргумента. Поэтому при построении графика для получения гладкой кривой вычисленные ранее приближения интерполируются подходящим полиномом. Расстояния между узлами определяются выбранным шагом сетки Ь На каждом шаге дифференциальное уравнение аппроксимируется конечно-разностным алгебраическим, где в качестве переменной выступает искомое значение функции в узле i. Заметим, что в нашем уравнении содержится производная первого и второго порядков. ВСПОМНИВ ее определение, знакомое читателю еще со школы. Приближенно можно записать: х =- :ь Если граничные условия заданы в форме производных, их также необходимо заменить разностными аналогами. Учитывая это, с помощью простых преобразований мы получим систему линейных алгебраических уравнений, называемую разностной схемой. Количество шагов N определяет количество алгебраических уравнений в системе: N+1 (с учетом граничных условий). К разностной схеме ггредъявляются следующие требования: во-первых, она должна наилучшим образом аппроксимировать дифференциальное уравнение, во-вторых, при стремлении длины шагах нулю решение разностной задачи должно сходиться к р*шсНИ1о дифференциальной задачи. Безусловно, для обеспечения сходимости необходима также устойчивость разностной схемы. Подставив левое граничное условие в первое уравнение, а правое - в последнее, можно обнаружить, что матрица коэффициентов при неизвестных А симметрична и трех-диагональна. Таким образом, задача сводится к решению системы АХ = В где В и х — вектор правых частей и неизвестных соответственно. Программа, реализующая изложенную идею, представлена ниже: Пример 14,25. Программная реализация разностной схемы для приведенной краевой задачи Задаем шггервал интегрирования, величину шага, коэффициенты уравнения, граничныеусловии и узловые точки расчетной сетки. Ь -а N:=500 а:=0 b:=20 h - - N u(t):=0.05 v{t) = -5 w(i) :=ain(0.05-t) 0 ... 154 155 156 157 158 159 160 ... 177 |












