Раздел: Документация

0 ... 157 158 159 160 161 162 163 ... 177

Пример 14.27. Решение одномерного уравнения теплопроводности (рис. 14.35)

F:=

(А 4- 30 L <- 40 п «- 30 т<- 500)

AL, а2к

п - 1т~1

for j е 0.. А - 1 for ie 1-L- 1

ь2;

Т <- 5 0,20

Т).0°

Ti.40-°

х:= 0.. 40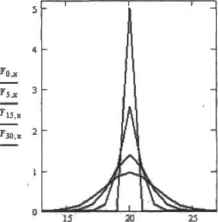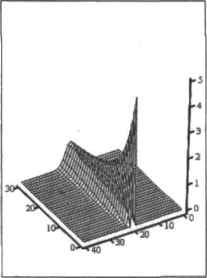

Рис. 14.35. Профили температуры нз разных временных слоях (с< 1 /2) и поверхность решения уравнения теплопроводности

Неверное решение, полученное с помощью разностной схемы при о 1 /2, представлено на рис 1436.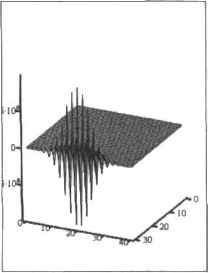

---

Рис. 14.30. Неверное решение, полученное с помощью разностной схемы при с>1/2

К сожалению, применение явных разностных схем ограничивается слишком малой длиной шага, используемой ими. Безусловной альтернативой, лишенной такого недостатка, является неявная разностная схема, обеспечивающая сходимость решения при любом значении параметра с.

Запишем конечно-разностную формулу, аппроксимирующую согласно неявной схеме уравнение теплопроводности:

Т -ТТ- 2Т + Т

i.j+l i,j 2 -— a--

kb2

Введем юхкрфициентс и перепишем разностное уравнение в следующем виде:

Принципиальным отличием неявных разностных схем является то, что изданном временном слое для поиска решения используются значения функции, рассчитанные на этом же слое, а не на предыдущем, как при вычислениях с помощью явных схем.

Сказанное выше иллюстрирует шаблон, изображенный на рис. 1437. Легко заметить, что для i-0.1,2...n и j-0,l ta последнее равенство приставляет собой систему линейных алгебраических уравнений, матрица которой, как и в случае крае» вых задач, симметрична и имеет трехдиагоналыгую форму.

С учетом этих особенностей представим программный вариант решения уравнения теплопроводности, используя неявную разностную схему.

---

—т—

Рис. 14.37, Шаблон аппроксимации уравнения теопопроводмости по неявной разностной схеме

Пример 14.28. Программная реализация неявной разностной схемы

(рис. 14.38)

T(A,L,n,m) ;=

1 с

а20

п - 1 m- 1

ЧU

for i 6 0.. п - I

for J € 1..П - I

Ь «- 1 + 2 с

(мп Л*-ь м «-ъ м. .*~ъ)

т. *-г 1

for t еО. n - I T<t+VlMlvC.T<0)

Т:-Т(30,30,ЗО.1О)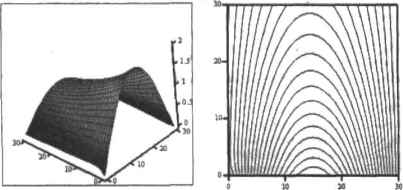

Рис. 14.3S. Поверхность и контурный график решения уравнения теплопроводности с помощь» неявной разностной схемы

0 ... 157 158 159 160 161 162 163 ... 177