Раздел: Документация

0 ... 158 159 160 161 162 163 164 ... 177

В начале программы определяется произвольный шаг по пространственной и временной координате, а также значение коэффициента я. Далее вводятся элементы матрицы М системы линейных уравнений, фапичныеТ0, Тп и начальные Tt условия. В конце на каждом временном слое t непосредственно вычисляются значения функции в узлах сетки. Заметьте, в примере решение получено при с—3, что подтверждает безусловную устойчивость неявных разностных схем.

Для решения линейных (параболических и гиперболических) и нелинейных одномерных уравнений в частных производных или их систем в Mathcad имеется вычислительный блок Given-Pdesolve, в основу работы которого положен метод конечных разностей (или метод сеток).

Итогом работы встроенной функции Pdesolve (ц, х, xrange, t, trange, [xptsj, [tpts]) является скалярная или векторная функция переменных х и t, представляющая собой решение уравнения или системы уравнений в частных производных. Для получения конечного результата алгоритм интерполирует значения, найденные в узлах сетки.

Задействовав функцию Pdesolve, нужно указать следующие параметры:

□и — искомая функции или вектор функций (в случае системы уравнений), не содержащие имен переменных:

□х — пространственная координата;

□xrange — вектор, задающий интервал поиска но пространственной координате. Содержит значения аргумента х На левой и правой фаннцах промежутка. Элементы вектора должны быть действительными числами:

□t — временная координата;

□trange — вектор, задающий интервал поиска по времени. Его элементы, представляющие собой значения переменной t на границах временного промежутка, могут быть только действительными числами;

□xpts — количество точек дискретизации по пространственной координате. Данный параметр позволяет пользователю влиять на процесс решения. Однако указывать его необязательно, в этом случае количество шагов в направлении х алгоритм определит автоматически наиболее оптимальным способом;

□tpts — количество точек дискретизации по времени. Параметр также не является обязательным для указания.

Прежде чем приступить к решению уравнения теплопроводности с помошью блока Given-Pdesolve, ознакомимся с некоторыми особеш гостя ми его использования.

□После слова Given вводится дифференциальное уравнение или система уравнений Неизвестные функции в уравнениях должны задаваться явно и содержать имена аргументов, например u(x,t).

□В отличие от вычислительного блока Given-Odesolve, производная функции по той или иной переменной указывается в виде нижнего литерального индекса («горячая» клавиша «.*). Например, nx.t) для первой и iiXjt) для второй производной.

□Для каждой неизвестной функции задается начальное условие u(x,0) и граничные условия, количество которых равно степени дифференциального уравнения. Гра ничвые условия задаются в форме Дирихле или Неймана. Например, u(0,t)-f(t) или u (0,t)*=f(t). Разумеется, границы интервалов, указанные вами в начальном и граничных условиях И в маркерах функции Pdesolve, должны совпадать. В противном случае будет выдано сообщение об ошибке.

□Знак равенства в уравнении, начальном и граничных условиях вводится с панели Boolean (или сочетанием клавиш Ctrl+-).

---

□Если уравнение содержит в левой части вторые частные производные, его необходимо представить в виде системы уравнений в первых производных. Например, чтобы корректно задать волновое уравнение ип(х.с)-сгим(х,1) в блоке Given-Pdesolve, следует выразить первую производную по времени через новую функцию n,( х д )-w(x .1) н записать систему: w,(x,t)-c1uo(x,t.>1 ut(x.L)-w(x,t), Для повой функции w(x,t) также задается начальное условие, например, w(x,0)=0.

□В блоке Given-Pdesolve наряду с дифференциальными уравнениями можно задавать и алгебраические. Например, для системы уравнений с неизвестными функциями u(x,t) и v(x,l) ограничение в виде u(x,t)+v(x,t)+M4x.i)-0 позволяет ввести в систему дополнительную неизвесткую функцию w(x.t), которая должна быть определена Pdesolve наряду с u(x,t) и v(x.t). Ограничения же в виде неравенств задавать нельзя

□При необходимости в контекстном меню функцин Pdesolve вы можете сменить модификацию аппроксимирующего метода, чтобы увеличить скорость расчета.

Решение одномерного уравнения теплопроводности с применением вычислительного блока приведено в примере.

Пример 14,29. Решение уравнения теплопроводности с помощью вычислительного блока Given-Pdesolve (рис. 14,39)

D:=0.05

L:=l

Т:=0.5

Given

nt(xTt) = Duxx(x,t)

ii(0,t)=0

u(L,l)=0

atx.O)

10 h

0

-1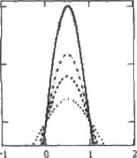

---

14.4.2. Гиперболические уравнения

В качестве примера гиперболического уравнения рассмотрим одномерное волновое уравнение, описывающее колебания струны С фиксированными концами.

Э2У 2 fcV

дС ах

Величина коэффициента с зависит от свойств материала струны.

Гиперболическое уравнение можно легко запрограммировать с помощью встроенных средств Maihcad, воспользовавшись все тем же методом конечных разностей". Для этого сначала определим начальные и граничные условия. При колебаниях концы струны не смещаются, поскольку закреплены. Это обстоятельство отражается в граничных

условиях:

V(t,0)=V0

V{t,L) = V0 i t й А

Начальные условия задают положение струны и ее скорость в исходный момент времени \:

V(0.x) = VHCX(x)

Ч(0.х) = 00 xL

Представим вторые производные, которые содержатся в обеих частях уравнения, в уже знакомой разностной форме:

Vj.w-a-vjti +VJ.J-, ? Vj,u-Vj,i +Уд.и

и приведем формулу к более наглядному виду, выразив значение волновой функции на следующем временном слое j+1 исходя из значений на предыдущих слоях] и j—1:

Нетрудно догадаться, что мы получили явную разностную схему, абсолютная устойчивость которой определяется параметром

2 к2.

а =

с - b

Решение сходится, если его значение не превышает S Четырехточечный шаблон рассмотренной схемы И узловые коэффициенты изображены на рис. 14,40.

Теперь, когда определены необходимые уравнения н параметры, приступим к реализации программы. Чтобы излишне ее не загромождать, не будем задавать величины шагов по обеим координатам, приняв известным значение параметра а н нулевую начальную скорость колебания струны.

0 ... 158 159 160 161 162 163 164 ... 177