Раздел: Документация
0 ... 159 160 161 162 163 164 165 ... 177 .УШ ш- —z— *Ч« JOV)V„ Рис. 14.40. Шаблон явной разностной схемы для волнового уравнения Пример 14.30. Разностная схема для решения уравнения колебаний (рис. 14,41) fori el.. 49 for j с 1..40 V. . *- O.fttsinf — j  Рис, 14.41, Поверхность решения волнового уравнения Так же успешно справляется с решением гиперболических и параболических уравнений и встроенная функция numoL Функция numol (xjendpts, xpts, t endpts, tpts, numjjde, num pae, pde func, pintt, bc func) возвращает матрицу размерности xpts tpts, которая содержит решения одномерного дифференциального уравнения в узловых точках сетки. В каждом столбце t( представлены значения функции но одной пространственной координате для данного временного слоя t,, В случае систем уравнений размерность матрицы увеличивается: xpts (tptsn), где п — общее количество уравнений. Решения для каждого уравнения системы по всем временным слоям располагаются соответственно слева направо. Заметьте, система может содержать не только дифференциальные уравнения в частных производных, но и алгебраические. Функция numol содержит большое количество параметров, поэтому к их заданию следует подходить особенно внимательно: □x endpts, tendpts — векторы, задающие интервал поиска решения по пространственной н временной координатам. Содержат два элемента, представляющих собой левую и правую гралнцу промежутка; □xpts. tpts - количество точек дискретизации расчетной области (x,t) (по координате х и t соответственно), в которых ищутся значения сеточных функций; □num pde, пшп рае - количество дифференциальных и алгебраических уравнений в системе. Еслн решается одно дифференциальное уравнение, первый параметр задается как 1. второй — 0; □pde fnnc — вектор функции переменных х, t, it, ut и и . количество элементов которого равно общему количеству уравнений в системе. Он должен содержать правые части уравнении в таком виде, чтобы в левых частях находились только первые производные функции по времени ur Для определения производных используется литеральный индекс очередность функций системы обозначается математическим индексом <[»; □pintt - вектор-функция переменной х размерности (nl) (где п — общее количество уравнений), задающая начальные условия для каждой функции в системе; □bc func — матрица граничных условий размерности (num pde-3). Задавая параметр bc func, обратите внимание на следующие особенности; 1)если уравнение, запнеанноедвнле pde func, содержит в правой части вторую производную, то в двух первых маркерах строки, соответствующей дан ному уравнению, указывается левое и правое граничное условие. Если они заданы в форме Дирихле, то в третий маркер необходимо ввести знак *D», для граничных условий в форме Нейману третий элемент строки записывается как «N»; 2)если в правой части уравнения, записанного н форме pde func, содержится только первая производная, то условие указывается только на одной границе интервала. В таком случае в соседний маркер вводится символ «NA», а в третий — «D»: 3)если уравнение не содержит производных в правой части, то соответствующая ему сгрока матрицы bcfunc должна выглядеть следующим образом: («NA» *NA» «О»), Другими словами, количество граничных условий для каждого уравнения системы должно быть равно порядку производной по пространственной переменной. Воспользуемся функцией numol для решения волнового уравнения. Обратите внимание на то. что в примере оно представлено в виде системы. Пример 14.31. Решение волнового уравнения с помощью встроенной функции numot (рис. 14.42) с := 5L := я х endpts:= xpts := 40 numjide := 2 tendpts ;= tpts := 30 T:=n 01 num pae:-0 p<te ttmc(x, l, U.Ujj, Uxx):- 2 с -u sin — pinitpt) ( "NA" "NA" "D" > be fuac(t) ;= pinit(0)0 Pinit(L)0 ТГ u:= пшпоЦх endptxpts,tendpts,tpts,num jde,пшпjwe.pde пше,pinit,bejunc) i;=0.. xpts 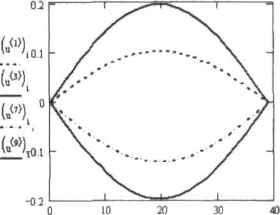 0 ... 159 160 161 162 163 164 165 ... 177 |












