Раздел: Документация

0 ... 160 161 162 163 164 165 166 ... 177

14.4.3. Эллиптические уравнения

Для дифференциальных уравнений н частных производных эллиптического тина it Math-cad имеются средства решения лишь одного из них - уравнения Пуассона, имеющего следующий вид:• ,

Лн2

-Т(х,у) + -Т(х,у)=-Г(х.у) dxdy

Чаще всего уравнение Пуассона (в прнведенеюй интерпретации) используют для описания некоторого стационарного процесса, например распространения температуры на плоскости вокруг источника (подчеркнем: здесь имеется в виду стационарный процесс распространения тепла; общее же уравнение теплопроводности записывается иначе). Впрочем, оно применимо и к целому ряду других физических явлений (например, в электростатике его используют дня описания напряженности электрического поля в двумерной области).

В Mathcad решение уравнения Пуассона ищется вузлах сетки размсрпостн(М + 1)х(М+1) (где М-2") точек, н углах которой должны быть заданы соответствующие граничные условия В том случае, если тепловой поток полностью рассеивается средой, то они должны быть определены как нули. Для описания этой наиболее простой ситуации в Mathcad существует специальная функция multigrid(F,ncycte), где:

□F - матрица размерности (М+1 )х(М +1) (М-2"), определяющая правую часть уравнения Пуассона, В случае описания стационарных процессов теплопроводности и ней вы должны он редел ить положение и силу источников (или поглотителей) тепла. В крайних элементах матрицы F следует задать соответствующие начальные условия (необходимость этого определения связана с тем, что таким образом вы со-пбшзеп? системе размерность сетки решения);

□ncycte — этот параметр определяет количество циклов, используемых численным алгоритмом на каждую итерацию. В большинстве случаев его достаточно определить как 2. хотя в случае плохой аппроксимации решения его можно задать и большим (естественно, целым) числом.

Приведем пример модели рассеяния тепла от одного источника при нулевых граничным условиях.

Пример 14.32. Решение уравнения Пуассона для случая полного рассеяния тепла

Заднем размерность аппроксимирующей сетки и краевые условия:

М :=25

РМ.М=0

Залаем координаты источника и его мощность:

Xsource:=13 Ysource:=13 Power := 123000

F"— Power

Xsource, Ysource

Решаем уравнение Пуассона с помощьюфушпшн multigriii (риг. 14.43):

T:=multigrid(-F,2)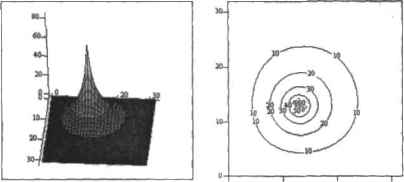

---

тт

Рис. 14.43. Поверхность и контурный график решения уравнения Пуассона

Обратите внимание на то, что матрица правой части уравнения Пуассона F должна быть задана с обратным знаком, что связано с ее физическим смыслом. С помощью функции multigiid можно промоделировать ситуацию, когда на одной плоскости располагаются несколько источников и но1Лотителей тепла. Для этого нужно просто правильно определить соответствующие элементы матрицы F.

Пример 14.33. Решение уравнения Пуассона при наличии нескольких источников и поглотителей тепла (рис. 14.44)

R:=23 TR,R :=0

г r := —165 t3 , > L50 т3 , := 50

R-2.—-R,-R-R,-R

24 44 2

Т :=multigrifl(-T,2)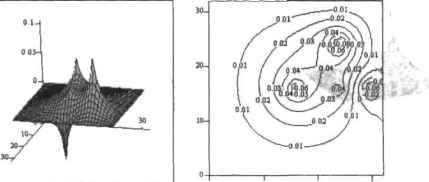

3030

ТТ

Рис. 14.44, Распределение тепла при наличии нескольких источников и поглотителей

<R R:=10° 2 2

---

j:=0..M

i:=0..M

i - >

M,M

b:=a = 0

с := a

23,12

: I

d :=a = 20

e := —4a F

-13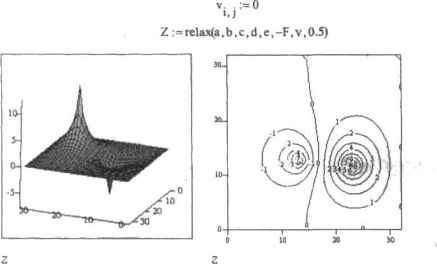

Рис. 14.45. Поверхность и контурный график решения уравнения Пуассона, построенные на основании расчета с помощью функции relax

В случаях, когда уравнение Пуассона имеет ненулевые значения краевых условии, найти ени решение можно с помощью спецналыtoii встроенной функции relax(a,cJ,e,F,v,rjac), где.

□a,b,c,d,e — квадратные матрицы одинаковой размерности, содержащие коэффициенты аппхжснмирующсй дифференциальное ураннение пятнточечной разностной схемы;

□F — квадратная матрица, соответствующая правой части уравнения Пуассона;

□v - квадратная матрица, содержащая граничные условия и начальные приближения для решения;

□rjac - спектральный радиус итераций Якоби. Может принимать значение от 0 до t и служит для характеристики скорости сходимости итераций.

Функция relax использует дли решения уравнений математической физики довольно распространенный алгоритм релаксации, описание которого т>ивод1ГГСЯ ниже. Приведем пример решения уравнения Пуассона с использованием схемы аппроксимации типа «крест».

Пример 14.34. Решение уравнения Пуассона с помощью функции relax (рис. 14.45)

M:=2S

0 ... 160 161 162 163 164 165 166 ... 177