Раздел: Документация

0 ... 156 157 158 159 160 161 162 ... 177

В общем виде дифференциальные уравнения второго порядка, которые описывают огромное количество разнообразных физических явлений, можно записать следующим образом:

A4+B.+C + D.E.U=F

бхck ay

Параметры реальных процессов, как правило, зависят от времени, поэтому око может выступать в качестве одной из переменных функции U. У равнение (как и сам процесс) в таком случае называется нестационарным (или неустановившимся),

Когда коэффициенты при производных — постоянные величины, уравнение линейно и в простейших случаях разрешимо аналитически. Если коэффициенты являются функциями того и in иного параметра, уравнение называется нелинейным и. как правило, не имеет аналитического решения.

Линейные уравнения математической физики подразделяются на три типа в зависимости от соотношения входящих в них коэффициентов, которое определяется физическим смыслом решаемой задачи:

□если Ьг-ас-0. уравнение называется параболическим;

□если Ы-ас>0. уравнение называется гиперболическим;

□если bJ-ac<0. уравнение называется эллиптическим.

В данном разделе мы рассмотрим простейшие примеры уравнений математической физики, относящиеся к трем указанным выше вилам тотистственно: одномерное уравнение теплопроводности, волновое уравнение и уравнение Пуассона. Но прежде поясним специфику постановки задач. Решением любого дифференциальиого уравнения в частных производных является функция нескольких аргументов, для каждого иэ которых необходимо задать область определения. Так как переменные характеризуют параметры реальных процессов, для них область определения всегда положительна. Если в качестве переменных функции U выступают пространствен наян временная координаты х и t, то начальные условия определяются как зависимости U(x) или ее первой производной на левой границе интервала существования t. Граничные условия, напротив, представляют собой зависимость V от времени t в крайних точках области определения пространственной координаты.

Принципы, лежащие в основе построения разностных схем существенно не отличаются от изложенных в подраэд. 14.3.2. Правда, задача несколько усложняется в связи с тем, что уравнение содержит производные функции по нескольким переменным. Поэтому даже в простейшем случае, когда функция U зависит всего от двух координат х и t, расчетная область покрывается двумерной сеткой, в узлах которой вычисляются соответствующие друг другу значения х и t. Теоретически разностную схему можно построить и для уравнений с тремя и четырьмя независимыми переменными. Например, волновая функция, являющаяся решением временного уравнения Ш редин г ера,

Э2 crV $V4

5" + J + J

ас sy а*

4x,y.z,t)v

on исываст движение частицы в пространстве (x.y.z) н времени t под действием потенциала V, то есть зависит от четырех аргументов. Тогда сетка будет поставлена в четырехмерном пространстве. Естественно, н таком случае во много раз возрастет коли-

---

чество разностных уравнений, аппроксимирующих искомую функцию на каждом шаге, а значит, и время расчетов Но можно поступ1ГГЬ и проще, перейдя от временного уравнения к стационарному, которое описывает положение частицы в фиксированный момент времени. Еще более упрощаются вычисления, если использовать набор дискретных значений одной из пространственных координат. Безусловно, выигрыш в сокращении времени расчетов окажется значительным, однако полученные таким образом решения уже не будут отражать реальной динамики квантового объекта.

14.4.1. Параболические уравнения

Рассмотрим в качестве примера параболического уравнения одномерное уравнение

теплопроводности

ЗТ 2 стЧ

I i?

описывающее процесс распределения тепла в неравномерно нагретом металлическом стержне, поверхность которого покрыта теплоизоляционным материалом. Будем пренебрегать толщиной стержня, предполагая, что в любой точке произвольно выбранного сечения температура постоянна (рис 14.33).

Тввлоюоллцкониый материал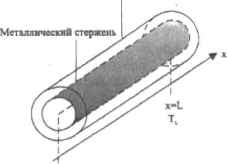

Т.

Рис. 14.33. Модель распространения тепла в неравномерно нагретом стержне

В течение определенного промежутка времени на концах стержня поддерживаются постоянные температуры Т( и TL, что необходимо указать в граничных условиях

T(t.0)-T0

T(t,L)=TL 0 Stfi А Начальное условие задает температуру стержня в момент времени г—0:

T(0,x)=T«cxtx) osxL

Коэффициент температуропроводности а является характеристикой материала, учитывающей его плотность, теплоемкость и теплопроводность Естественно, зги параметры

---

могут меняться прн различных температурных режимах, и в реальных условиях а зависит от температуры. Однако для упрощения задачи флуктуациями свойств вещества можно пренебречь.

Теперь, когда задано уравнение, описывающее процесс диффузии тепла, и нее i ieo6xo~ днмые условия, можно приступить к построению разностной схемы.

Для этого нанесем на расчетную область сетку, в узлах которой будем искать функцию Т — температуру участка t в момент времени j. Заметим, что длина шага к и h по временной н пространственной координатам] Н i может и не совпадать. Другими словами

тм = т, + ь

Далее запишем исходное дифференциальное уравнение в конеч]to-разностной форме (аналогично решению краевой задачи в предыдущем разделе):

2

Tj-fl,i~TJ,i а Tj,i-1 " 2 Tj.i + Tj.i+1

к =h2

Общая температура стержня при t-j будет решением уравнения на временном слое j, Обратите внимание на то, что температуру в следующий момент времени j + 1 можно выразить, исходя из ранее найденных значений Т в трех соседних узлах i предыдущего временного слоя]. Такого рола схемы называются явными.

а2 к

Vlti=-TjM+(l-2.c).T.j+cTj>liWc= —

а

Более наглядно явная схема аппроксимации для уравнения теплопроводности изображена в виде шаблона на рис. 14.34.

с-Т,.,

о-ад-Tj,

Рис. 14.34. Шаблон явной разностной схемы для решений уравнения теплопроводности

Решение, полученное с помощью приведенной разностной стрму, представлено ниже в виде npoq>aMMbi.

Огметим одну очень важную особенность, которую следует учитывать при вводе параметров задачи. При определенном их сочетании явная разностная схема становится неустойчивой. Это связано с тем, что ошибка аппроксимации, полученная на одном слое, увеличивается при переходе к следующему. Когда же разностная схема устойчива, в процессе вычислений ошибка уменьшается. В нашем случае показателем сходимости решения является множитель с. Схема устойчива, если он принимает значения от 0 до S. В противном случае решение расходится (см. второй рисунок в примере 14.27).

0 ... 156 157 158 159 160 161 162 ... 177