Раздел: Документация

0 ... 155 156 157 158 159 160 161 ... 177

:=0

:= I

im 1.. N- I tj :=а +th

Определяем для системы разностных ураинений трехд и а тональную матрицу коэффициентов прн неизвестных.

А. .:=2+ h2-v

4*1 2

-ь

A:=Bubmalrix(A,l,N- 1,1, N- 1)

Задаем вектор правых частей

во-ь2-ч11)+ь(Нс0+1)

for i€ 1-N-3 2

B.-h-w(t.+ ])

В

Решаем систему разностных уравнений

х:=> leolvetA.B)

х:= 8Еаск(ха,х,х) Результат работы разностной схемы представлен на рис. 14.31.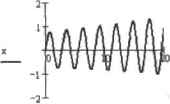

Рис. 14.31. Результат работы разностной схемы

Отметим некоторые особенности построенной разностной схемы. Вторая Пх>изводная должна быть в первой степени и не содержать каких-либо сомножителей, краевые условия должны быть поставлены строго на границах интервала поиска. Коэффициенты при остальных слагаемых, а также свободный член уравнения в общем случае могут являться функциями, поэтому и программе заданы в виде n(t), v(t) и w(t). Точность варьируется в зависимости от количества шагов, однако не следует забывать, что при слишком

---

большом их увеличении резко возрастает время расчетов, значительная часть которого используется функцией IsoLve. Связано это с тем, что встроенному алгоритму приходится работать с матрицами больших размеров. В пашем случае, когда количество узловых точек равно 500, матрица А имеет размерность 500-500. Нетрудно понять, что при увеличении N в арифметической прогрессии скорость вычислений будет падать в геометрической прогрессии. Например, уже при N=1000 расчет длится недопустимо долго,

К счастью, решить возникшую проблему довольно просто. Как известно, самым популярным алгоритмом решения систем линейных алгебраических уравнений является метод поеледовател ьного исключения Гаусса. В классической форме для N-1 уравнений системы он требует порядка гР арифметических операций. Однако для систем, содержащих матрицы особой структуры имеется множество вариантов этого алгоритма, которые позволяют во много раз понысить его быстродействие. Выше мы упоминали, что матрица А имеет ленточную структуру: только главная диагональ и две соседние содержат ненулевые элементы (рис. 14.32).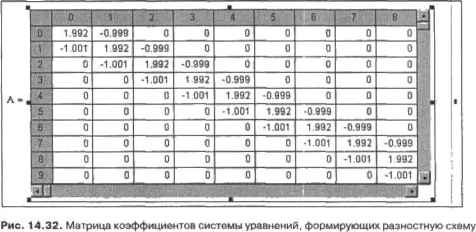

Для решения систем с подобными матрицами существует модификация алгоритма Гаусса, называемая методом прогонки. Замечателен он тем, что для нахождения корней системы N—1 уравнений требует порядка N операций, в отличие от стандартного алгоритма. Попытаемся разобраться в сущности метода прогонки и напишем соответствующую программу, которая наверняка окажется полезной для читателя, столкнувшегося с необходимостью решения систем уравнений стрехднатоналыюй матрицей. Любое решение, полученное методом прогонки, описывается уравнением

x-f = о-н-i • Xj+l + Pi+ i

где ct,,,, Pkl - прогоночные коэффициенты. Они определяются на первом этапе работы алгоритма, называемого прямым ходом прогонки. В классическом варианте метода Гаусса этому этапу соответствует приведение матрицы к треугольному виду. Обратим внимание, что, согласно уравнению, предыдущий корень вычисляется исходя из последующего. Такая последовательность называется обратным ходом алгоритма прогонки, в процессе которого непосредственно ищется вектор решений. Описанные действия

---

представлены ниже в виде программы. Заметим, что скорость расчета значительно возрастает при замене функции (solve в примере на наш алгоритм.

Пример 14.26. Алгоритм прогонки

If -*

х:=

О, 1

Ло.о

for i б 1.. N - 3

-А

<Ч+-1

i.l+I

А. .+ А

H-l.tQi

Рн-I

-А. . .fjj + В. . H-l,iГ i,0

А. . + А. . ,-а

~AN-2,N-3Pn-2+BN-2,0

AN 2iN 2 + AN-2,N-3aN-2 for ie N-3..0

*N-2

x. i

"k-lVl + Pi+1

Метод прогонки также используется для решения систем разностных уравнений, аппроксимирующих дифференциальные уравнения в частных производных. Об этой фуппе дифференциальных уравнений мы поговорим в следующем разделе.

14.4. Дифференциальные уравнения в частных производных

Пожалуй, мы будем пе столь уж неправы, назвав дифференциальные уравнения а частных производных самым сложным разделом не только теории численных методов, но п всей математики в целом. Уравнения эти, называемые также уравнениями математической физики, с удивительной точностью описывают самые разнообразные реальные процессы, начиная от колебаний струны п заканчивая всевозможными явлениями в биосфере. Поэтому подавляющее большинство современных разработок, которые ведутся специалистами по численным методам, относятся именно к области дифференциальных уравнений в частных производных.

Дли численного решения дифференциальных уравнений в частных производных существует множество разностных схем, вид которых определяется тем или иным типом уравнения. Чтобы понять принципы работы встроетнлх средств Mathcad, возможности которых в решении уравнений математической физики, начиная с 11 версиН программы, значительно расширились, мы приведем дополнительно примеры построения разностных схем для наиболее известных уравнений.

0 ... 155 156 157 158 159 160 161 ... 177