Раздел: Документация
0 ... 153 154 155 156 157 158 159 ... 177 По аналогичному принципу преобразуется и второе уравнение; -g У2 dr. dtJ Теперь, когда система задана в корректной форме, приступим к се решению с помощью функции sbval. Краевые условия определим такими же, как в примере 14.27. х(0) = 0х(5)=Ю0 у(0) = 0у(5) = 0 Задаем вектор приближений для искомых неизвестных начальных условий на левой границе интервала и границы самого интервала: Определяем вектор-функцию D для системы уравнений: ( 0 -О t0:=0 tl:=5 D(t,y) ;= -9.81 Задаем вектор значений функций системы tra левой фашше интервала; Ioad(t0,z):= о; Задаем краевые начальные условия на правой границе интервала; score(tl,y) юоЛ V Вычисляем недостающие начальные условия на левой границе К1ттсрвала: z:=sbva](z,tQ, tl.D,load,score) J 10 ) \2A.S25J Решение полученной задачи Коши с помощью метода Рунге-Кутта с фиксированным шагом (рис. Н.2Э): у0:= load(tO.z) R := rk.fixeffl:yO,t&; 5.1000.D) 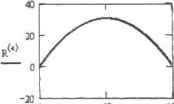 D50 Рис. 14.28. Траектория движения тела, брошенного под углом к горизонту {решение краевой задачи идентично полученному с помощью вычислительного блока) Обычный метод пристрелки, реализуемый функцией sbval, эффективен ЛИШЬ В случае непрерывности первых производных функций решения. Многие же физические модели подразумевают наличие точек разрыва на кривых искомых функций, н использовать для решения таких задач стандартный метод стрельбы нельзя. Однако решить подобные системы все же возможно, если вести пристрелку сразу из обеих границ интервала. В Mathcad имеется специальная встроенная функция bvalfit(zl,z2.xO,x1,xf,D,loadl,loadZ,score), реализующая эту идею, Так как принципы, лежащие в основе работы bvalfit. довольно непросты, то н параметров для нее нужно задать рекордное количество — иелых девять: □zi — вектор исходных приближений для недостающих начальных условий на левой границе интервала; задается точно так же, как в случае функции sbval; □z2 — вектор приближений для недостающих условий на правой границе интервала (одно иэ принципиальных отличий bvalfit от sbval заключается в том. что она определяет недостающие для корректного задания задачи Коши параметры для обеих границ расчетного промежутка) О хО - левая граница промежутка решения; □xl — правая граница промежутка решения; □xf — точка внутри речетного интервала я которой происходит сшивка левого и правого решений. Исходя из математического смысла встроенной функции bvalfit, чаще всего xf — это точка, в которой производная функции решения имеет разрыв: □D(x.y) — вектор-функция, описывающая дифференциальное уравнение или систему дифференциальных уравнений. Задается так же, как для всех рассмотренных нами ранее функций решения систем ОДУ; □load l(xO.zi) — векторная функция, описывающая начальные условия на левой границе интервала. Количество ее элементов должно совпадать с количеством уравнений в системе. Известные приближения должны быть заданы численно, искомые — соответствующими элементами вектора П; □load2(xi,z2) — вектор-функция для условий па правой границе интервала. Задается точно так же, как load V. □score(xf,y) — векторная функция, описывающая поведение функций решений в точке xf. Обычна является просто условием сшивки и определяется равной вектору у. Однако возможны и более сложные условия, задающие, например, разрыв на искомой кривой. Результатом работы функции bvalfit является матрица нз двух столбцов, в первом из которых содержатся искомые приближения для правой границы интервала, а во втором — соответственно для левой, Чтобы затем корректно визуализировать результат расчета, соответствую щи с кривые должны быть составлены из двух различных фрагментов, сшитых в точке xf. Сделать это можно простым решением двух задач Коши: одной — на промежутке от хО до xf. Другой — на отрезке OTXf дох1. Естественно, что при атом нужно использовать различные начальные приближения Воспользуемся функцией bvalfit, чтобы решить следующую задачу. Пружинный маятник совершает колебания, В определенный момент времени к нему подвешивают груз. Необходимо определить, как изменится характер колебаний маятника вследствие изменения его массы, На пружинный маятник массой т, совершающий колебания, действуют две противоположно направленные силы: сила притяжении F-mg и сила Гука F--ltx,(rae к — коэффициент жесткости пружины, х — смещение маятника), С учетом второго закона Ньютона запишем суперпозицию этих сил как m-i = к х + mg Сократим обе части равенства на т: к а =---х+ в т Представив ускорение а в дифференциальной форме, мы получим уравнение колебаний пружинного маятника tS2 к -,x{t) =--х + 8 dt2 m Чтобы получить краевую задачу, функция решения которой имеет разрыв, зададим краевые условия и условия изменения характера колебаний. Пусть колебания маятника наблюдались в течение десяти секунд. В начальный момент времени смещение маятника было равно 5, в конечный - 10. Груз, подвешенный на четвертой секунде наблюдения, увеличил массу маятника в 15 раз. Определить, как меняется характер колебаний на протяжении всего времени наблюдения. Решение полученной задачи представлено в примере 14.24. Пример 14.24. Использование функции bvalfit в решении задачи об изменении характера колебаний маятника Зшшсм параметры колебательной системы - жесткость пружЖЯМ И ИСХвде*уи массу ШМП HHJGK к:=100га:=5 Определяем приближения для неизвестных начальных условий - скорости колебаний: zl0:=020 Залаем границы временного интервала: Й:=0И:=10 Определяем точку сшнвки tf: tf:=4 0 ... 153 154 155 156 157 158 159 ... 177 |












