Раздел: Документация
0 ... 152 153 154 155 156 157 158 ... 177 Техническая реализация метода стрельбы в Mathcad совсем не сложна, и написать соответствующую программу можно всего за несколько минут. Однако делать этого нет никакого смысла, так как в системе уже имеются встроенные функции, позволяющие преобразовывать краевые задачи в форму задач Коши. Приведем решение описанной выше краевой задачи а колебаниях с помощью вычислительного блока Given-Odesolve. Пример 14.21, Решение краевой задачи о колебаниях с помощью вычислительного блока (рис. 14.27) Given Х(0) = О -4-X(t) + X(t) = 0 dl 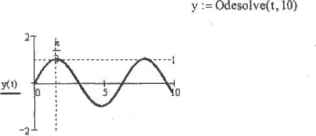 Рис. 14.27. График решения краевой задачи о колебаниях Как вы можете ааметить из приведенного примера, никаких особых отличий между решением ОДУ в краевой форме и форме Коши с помощью вычислительного блока нет. Единственное, вы должны корректно задать начальные условия: так, например, вы не можете при решении уравнения второго Порядка на одной границе определить значение функции, а на другой - ее производной. Соответствующие начальные условия должны быть штределены либо только функциями, либо только производными. При решении ОДУ более высоких порядков для задания краевьгх условий появляется довольно значительное количество вариантов. Это связано с тем. что различным может быть как распределение условий между границами, так И относительное количество производных различных порядков. Так, например, можно найти кривую корня ОДУ 4-го порядка, если три 11ачальных условия определены на правой границе, и только один — на левой. Всего же вариантов задания граничных условий для такого уравнения могут быть десятки. Как н для систем ОДУ, заданных S форме Коши, вычислительный блок Given-Odesolve может находить решения для систем дифференциальных уравнений произвольного порядка с краевыми условиями. Приведем пример простейшей краевой системы ОДУ, описывающей траекторию движения тела, брошенного под углом к горизонту, В лю- •о действует только сила притяжения F-mg. еле m - масса одного падения (9,61 w/cJ). Тогда, с учетом второго закона Нью-•а оси х иуможио представить в виде следующих уравнений: част .отовун № dt2 = о d2y 6С -m-g / части уравнении на т. мы получим проекции вектора ускорения на оси х говую систему дифференциальных уравнений осталось дополнить крае-.Овняын: пусть время полета составило пять секунд, за которые тело персмес-4а расстояние 100 метров. Решение полученной краевой задачи представлено .мере 14.22. ример 14.22. Решение краевой задачи о теле, брошенном под углом к горизонту, с помощью вычислительного блока (рис. 14.28) Given х(0) = о х<5)= 100 у(0) = 0 4ф dt у(5)»0 - -9.81 -ijy(t) dt (y):"°deeelV{(y) t,5 t := 0,0.01.. 5 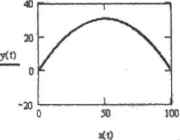 Рис. 14.2В. Траектория движения тела, брошенного под углом к горизонту Помимо вычислительного блока, для решения краевых задач в Mathcad имеются две встроенные функции, реализующие метод пристрелки. Первая из ннх, более простая и важная практически функция sbval(z.xOxl,d,toadjcore), осуществляет поиск недостающих параметров для двухточечных краевых задач. Данная функция требует определения весьма значительного количества параметров: □ г. Вектор приближений, в котором вы должны определить исходные значения для недостающих на левой границе условий. К заданию этого параметра стоит подойти 480 * Глава 14. Дифференциальные уравнения > .......................\ предельно аккуратно, так как верный вы1Ц, мрцдлу знач1тяьнс« милою ю точность □хО Левая граница интервала решения;\ □xl. Правая граница интервала решения**°4ъ • □D{x,y). Векторная функшчя, описывающая лилейноедиф4 а. • или систему линейных дифференцвалышх уравнении. За. при использованми рассмотренных нами ранее иптиюнт*. чеиных для решения ОДУ и систем ОДУ в форме задачи Ко, □load(xCU). Векторная функция двух переменных, описывают* па левой границе промежутка. Прелставляетсо&п! вектор ни количество уравнений системы), каждый из которых является к-1 соответсгвующей функции вектира у параметра D. Если началь, £* некоторой функции неизвестно, в качестве элемента load следуй, величину на вектора приближений г,\ □scorefxl.y). Векторная функция, служащая для задашь правых гранич* При ее определении следует учитывать одну очень нажную и совершенно неочеьк„ ную техническую сгсобекносгь: элементы вектора score должны быть заданы как разности начальных значений н соответствующих им значений функций. Все дело втом, что алгоритм, лежащий в основе функции sbval, использует текущие величины score в качестве меры точности подобранных приближений. Результатом работы функции sbval является вектор с найденными значениями недостающих для представления системы дифференциальных уравнений в форме задачи Коши начальных условий, Для того же, чтобы решить непосредственно ОДУ или систему ОДУ. следует использовать одну из стандартных встроенных функций, например rkfixed. При этом в качестве ее параметра уО можно использовать уже определенную выше функцию load (обозначив, естественно/ вектор результата как z) (см. пример 14.23). Читая описание параметров функции sbval, вы, наверное, испытали легкую дрожь от чрезмерного обилия Переменных, векторов, функций и постоянных. Однако на самом деле в решении краевой задачи для ОДУ или системы ОДУ с использованием данной функции нет ничего гложлого. Убедимся в этом иа конкретном примере — решим рассмотренную выше краевую задачу о движении тела, брошенного иод углом к горизонту. Пример 14.23. Решение краевой задачи о движении тела, брошенного под углом к горизонту, с помощью функции sbval Чтобы восполыпвлться функцией sbval, сведем пишу систему дифференциальных уравнений второго порядка (см. пример 1422) к системе дифференциальных уравнений первого порядка, левые части которых содержат только производную. Правые же части нам нужно будет задать как векторную функцию D (правой части каждого уравнения ставится в соответствие элемент у, являющегося параметром D). Первое уравнение можно преобразовать к системе на двух уравнений первого порядка, введя новую функцию z{t). равную первой производной x(t) по к 4-x(t)=z(l) у dt1 0 ... 152 153 154 155 156 157 158 ... 177 |












