Раздел: Документация
0 ... 13 14 15 16 17 18 19 ... 87 2.5. Учет насыщения магнитной системы в математическом описании асинхронного двигателя В предыдущих подразделах при составлении математического описания асинхронного двигателя считалось, что насыщение магнитной системы отсутствует. Это выражалось в постоянстве коэффициентов индуктивности Lm, Lx и L2. Машину, в которой такое допущение считается приемлемым, называют ненасыщенной. С одной стороны, рассмотрение ненасыщенной машины в ряде случаев, например при ее описании в виде схемы замещения, позволяет получить сравнительно простые и удобные для расчетов формулы и структурные схемы. С другой стороны, достижимая при таком упрощении точность расчетов может оказаться достаточной с учетом того, что номинальный поток соответствует рабочей точке на характеристике намагничивания, близкой к линейной части, где эффект насыщения магнитной системы проявляется сравнительно слабо. Тем не менее, когда при уточненных расчетах оказывается желательным учесть насыщение, это может быть сделано [53]. С достаточной степенью точности можно считать, что насыщение проявляет себя только в изменении коэффициента, связывающего главный магнитный поток (полезный поток в зазоре) с намагничивающим током (током в намагничивающем контуре схемы замещения), а связь между потоками рассеяния статора и ротора и соответствующими токами остается такой же, как в не- 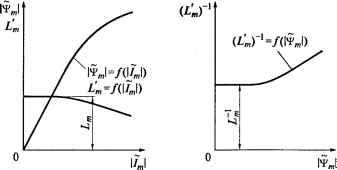 аб Рис. 2.7. Характеристика насыщения магнитной системы асинхронного двигателя: а - характеристика намагничиванияfm = ffl/m) и зависимость Ц, = т); б - обратная зависимость (Ц,)1 = /"¥„,\) насыщенной машине и характеризуется постоянными индуктив-ностями рассеяния статора и ротора Llc и L2o. Характеристика намагничивания машины \т\ = /(Ли)> как зависимость между модулями пространственных векторов главного потокосцепления и намагничивающего тока, показана на рис. 2.7, а. При записи уравнений, описывающих насыщенную машину, эту связь удобно представить в виде зависимости ш I J> \т I * ml -Ми \лm\у где Lm - переменный коэффициент индуктивности, характеризующий нелинейную связь между главным потокосцеплением и намагничивающим током. Если нужна обратная зависимость, то можно записать /т = = (Lm)1 \Vm\- Выбирая в рабочей зоне характеристики намагничивания ряд значений /т и определяя соответствующие им значения \¥т\, можно рассчитать точки для построения зависимости (Lm )ч = / (Itml), показанной на рис. 2.7, б. Коэффициент Lm уменьшается по мере насыщения магнитной системы, а коэффициент (Lm) 1 - возрастает. Это характеризует то обстоятельство, что для получения некоторого значения потокосцепления х¥т в зоне насыщения требуется больший намагничивающий ток, чем для получения того же значения потокосцепления в ненасыщенной машине. В части характеристики намагничивания, которую можно считать линейной, выполняются равенства Lm=Lm и (Lm) = Lml. Из этого следует, что, в отличие от ранее рассмотренных структурных схем, в которых фигурировали токи статора и ротора и полные потокосцепления, для рассмотрения насыщенной машины модель двигателя надо перестроить так, чтобы в ней присутствовали главное потокосцепление и намагничивающий ток. Для получения такой структурной схемы при произвольном расположении координатной системы а-Р относительно системы пространственных векторов используем первые два уравнения системы уравнений (1.23). Имея в виду, что полные потокосцепления статора и ротора отличаются от главного потокосцепления соответственно на величины потокосцеплений рассеяния, определим их пространственные векторы: = 1/m + LlaIu (2.27) 51 и выразим из первого уравнения ток статора, а из второго - главное потокосцепление, вектор которого в ненасыщенной машине связан с векторами токов выражением = Lm {Ji + /2) = LmIm, где /„, = /,+ /2. При учете насыщения связь между Чт и 1т представляет собой нелинейную зависимость =LmIm, или /m=(i;)-Tm.(2.28) С учетом выражений (2.27) и (2.28) система уравнений для пространственных векторов во вращающейся системе координат будет иметь вид: рЧ>2 =-I2R2-jiop%; Ii=(4,i-Vm)/Lla; ~ У2 ~ L2ah> I2 = 1щ ~ 1\\ Структурная схема строится на основании выражений: PVla = "la - lla + «ОзлУ PVip = "ip ~ llp - Озла! p\y2a = -R2i2a +ropv2p; рщр = -Дг20 -cop\i/2a; la = (Via - Vma)/ila;lp = (Vlp - Vn®)/L\„\(2.29) Vma = 4>2a 2с ha,Vmp = V2p 2а г2р! (2a = lma ~ ha\*2p = mP ~ ip> ma = (An) \j/ma;/mp = (Lm) Vmp, 0 ... 13 14 15 16 17 18 19 ... 87 |












