Раздел: Документация
0 ... 16 17 18 19 20 21 22 ... 87 Так же, как это было сделано при математическом описании асинхронного двигателя, введем в рассмотрение систему координат d-q, связанную с ротором и вращающуюся вместе с ним. Однако между системами координат d-q в асинхронном и синхронном двигателях есть существенное различие, состоящее в том, что в первом случае эта система координат вращается в электрическом пространстве со скоростью ротора /?псо = со0эл - юр> которая во всех режимах, кроме режима идеального холостого хода, отличается от синхронной скорости, а во втором случае ее скорость в электрическом пространстве всегда равна синхронной скорости ращ - со0эл. Таким образом, система координат d-q в математическом описании синхронного двигателя играет ту же роль, что вращающаяся с синхронной скоростью система координат а -Р в математическом описании двигателя асинхронного. Поскольку обмотка статора синхронного двигателя принципиально не отличается от статорной обмотки асинхронного двигателя, уравнение равновесия напряжений статора (2.11) может быть непосредственно использовано в математическом описании синхронного двигателя, если входящие в него пространственные векторы представить через их проекции на оси координат: U\ = iiw + Мд; /, = iu + jiXq; ¥, = уи + jylg. В отличие от асинхронного двигателя, обмотка ротора которого обтекается трехфазным переменным током с угловой частотой, равной сор, в обмотке возбуждения синхронной машины протекает постоянный ток. Напряжение на обмотке возбуждения щ, ток в ней if и потокосцепление ротора могут быть представлены пространственными векторами, неподвижными относительно ротора и вращающимися вместе с ним, а следовательно, вместе с системой координат d-q. В этом смысле они не отличаются от пространственных векторов, образованных в результате рассмотрения трехфазной системы статорных напряжений, токов и потокосцеплений. Поэтому, направив ось вещественных d по оси обмотки возбуждения, т. е. по вектору потокосцепления ротора и совпадающим с ним по направлению векторам напряжения и тока возбуждения, роторные величины, связанные между собой равенством uf= R/i/ + pf можно рассматривать как проекции пространственных векторов на ось координат d. Для рассмотрения связи между токами и потокосцеплениями Удобно воспользоваться моделью двигателя, представленной на Рис. 3.1. В модели трехфазная обмотка статора заменена двумя, неподвижными относительно вращающейся системы координат d~ q, обмотками, которые характеризуются активным сопротивлением Rx и индуктивностями Lldn Llg. Оси этих обмоток направлены по осям координат d и q. К ним приложены напряжения Рис. 3.1. Модель синхронного двигателя во вращающейся системе координат постоянного тока по прямой и квадратурной осям uXd и uXq, в результате чего по обмоткам протекают токи iXd и iXq. К обмотке ротора с сопротивлением RfW индуктивностью приложено напряжение возбуждения ufi ток в ней обозначен как if. Из рис. 3.1 видно, что при принятом направлении осей координат потокосцепление статора по оси d определяется токами iXd и if, а по оси q - только током iXq. С учетом сказанного математическая модель электромагнитных процессов в синхронном двигателе без демпферной обмотки может быть представлена в виде системы уравнений для проекций обобщенных векторов на оси вращающейся системы координат: "и = R\i\d + PVid ~ fcW/ig;(3.1) "lg - Rlhq + PVlq + ЩэлV\dl(3-2) uf = Rfif + P4> f;(3.3) Vfu = LXdiXd + Md/if;(3.4) Vig = LXqiXq;(3.5) 4f=Lfif+Mfdild,(3.6) где Rx, Rf- сопротивления фазы обмотки статора и обмотки возбуждения соответственно; LXd, LXq и А/ - полные индуктивности обмоток статора по осям d и q и полная индуктивность обмотки возбуждения соответственно; Mdf - коэффициент взаимной индукции между обмоткой возбуждения и обмоткой статора по оси d, Mdf= Mfd. Обычно в каталогах на синхронные машины параметры даются в относительных единицах. Поэтому целесообразно при рассмотрении математического описания электромагнитных процессов в синхронном двигателе также перейти к относительным единицам, т. е. нормировать уравнения, входящие в его математическое описание. Базовые значения, относительно которых выполняется нормирование, должны быть выбраны так, чтобы максимально 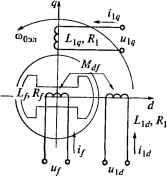 упростить исходные уравнения при сохранении их соответствия физическим процессам, происходящим в двигателе. Для нормирования уравнений (3.1)...(3.6) базовые значения величин выбраны следующим образом [47, 60]: базовое напряжение на статоре £/1б = £/1н V2 = Il6Z6; базовый ток статора /1б = V2/lH; базовая угловая частота напряжения на статоре со0эл.б = базовое потокосцепление обмоток статора Т1б = £71б/со0эл.б > базовое сопротивление Z6 = UX6/IX6 = со0эл.бб; базовая индуктивность обмотки статора L6 = W/I; базовый ток возбуждения Ьъ---- = -х-\ базовое напряжение возбуждения U/6 = Rflf5; базовое потокосцепление обмотки возбуждения Ч/ = Lflf5. В этих выражениях базовая индуктивность статора определена, как индуктивность, при которой базовый ток статора создает базовое потокосцепление, а базовый ток возбуждения - как ток в обмотке возбуждения, при котором на холостом ходу при базовой скорости двигателя индуцируется базовое напряжение. Индексом «н» помечены номинальные значения величин. Системы уравнений (3.1)...(3.6) в целях перехода к относительным единицам преобразуются делением всех переменных на их базовые значения, а там, где это требуется, умножением на соотношения параметров, равные единице:
+ p U\5 СОоэл.бU\5 Шоэл.б , Vlg Шрэл.б ЮрзлЫ Юрэл.б . Р тттт У\б Ш0эл.бU16 Щэп.б RfI + Р Я/б W\d Lxdixd + Mdfij Wig L\qi\g . б-чб 0 ... 16 17 18 19 20 21 22 ... 87 |












