Раздел: Документация
0 ... 18 19 20 21 22 23 24 ... 87 ния {/[ = Ux приводит к изменению соотношения между его проекциями на оси вращающейся системы координат d-q, которые в относительных единицах определяются как щд =-£7, sin 6; Угол нагрузки, измеряемый в радианах, определяется через интеграл от разности мгновенных значений скоростей поля статора и ротора в электрическом пространстве, существовавшей в течение времени переходного процесса, связанного с изменением нагрузки: Через скорости в относительных единицах выражение для угла 6 в радианах запишется в операторной форме: Структурная схема электропривода с синхронным двигателем без демпфирующей обмотки во вращающейся системе координат и при питании от источника бесконечной мощности показана на рис. 3.3. 3.2. Статические характеристики электропривода с синхронным двигателем В основу рассмотрения статических (так называемых угловых) характеристик синхронного двигателя, представляющих собой зависимость электромагнитного момента в установившемся режиме от угла нагрузки, положено выражение для момента двигателя А/д = /1? - ф1? ild. Поскольку в установившемся режиме ток в демпферной обмотке отсутствует, выкладки, приведенные далее в этом подразделе, справедливы как для двигателя без демпферной обмотки, так и для двигателя с демпферной обмоткой. Подставив в формулу для момента значения проекций вектора тока статора ild = (yld - if)/xd и Tlg = щд/хд, получим Как следует из векторной диаграммы (см. рис. 3.2), проекции вектора потокосцепления статора могут быть записаны через мо- щд =t7,cos6. 6 = /(«Оэл -Aiw)df. о е = Юоэл.б(и0 -а)/р. 3 Соколовский 65 дуль вектора в относительных единицах Ч1, = Ч* i и угол нагрузки в виде: v/w = 4х, cos6; Wig = Ч7, sine. С учетом этого выражение для момента при известных токе возбуждения и потокосцеплении статора можно определить как сумму двух слагаемых: ЧУ/ . . ч> xd щ2 f Мд = --sin6 + J 1 Хд Xj sin 26.(3.8) Поскольку в неявнополюсном двигателе индуктивные сопротивления по прямой и квадратурной осям равны друг другу {xd =х?), то первое слагаемое в формуле (3.8) представляет собой электромагнитный момент двигателя с неявнополюсным ротором, а второе получается вследствие неравенства значений индуктивных сопротивлений по прямой и квадратурной осям системы координат в явнополюсном двигателе. Из первых двух выражений системы уравнений (3.7) в установившемся режиме (т.е. при р - 0) и при пренебрежении активным сопротивлением обмотки1 статора (Д = 0) можно получить связь между потокосцеплением j и напряжением на обмотке статора: Vi, = -"и/® о; Wid = й„/б0; Ч7, = Uj(b0, где £7, - модуль вектора статорного напряжения. Тогда выражение для момента двигателя можно записать в видя Vjfa.Utfl 1 Мп =--sin6 + <a0xd2 cog =--rE- sin 26.(3.9)1 Хд Xd I По выражению (3.8) или (3.9) может быть построена угловая характеристика синхронного двигателя (рис. 3.4). Отмеченная на характеристике точка 0 - точка идеального холостого хода. По мере увеличения нагрузки на валу двигателя вектор потокосцепления ротора вместе с ротором сдвигается в электрическом пространстве в сторону отставания от вектора потокосцепления статора. Таким образом, угол 6 является отсчитываемым в электрических радианах во вращающейся системе координат углом смещения ротора от положения, соответствующего идеальному холостому ходу двигателя. Если значения момента в двигательном режиме считать положительными, то двигательному режиму соответствует часть характеристики вправо от точки идеального холостого хода, а генераторному - влево. Часть характеристики, на которой увеличение угла 6 сопровождается ростом момента двигателя (участок OA), соответствует устойчивой работе двигателя с синхронной скоростью. Если после достижения моментом значения Матах момент нагрузки еще возрастет, то электромагнитный момент двигателя не увеличится, а уменьшится, и двигатель выпадет из синхронизма. Для генераторного режима устойчивый режим характеризуется участком ОБ. Для двигателя с неявнополюсным ротором критическим углом нагрузки является угол = ±п/2. Для двигателя с явнополюсным ротором значение критического угла нагрузки может быть определено из выражения (3.9) в результате исследования его на экстремум. Приравнивая нулю частную производную ЭЛ/д/ЭВ и имея в виду, что cos26 = 2cos26 - 1, можно получить квадратное уравнение для определения критического угла нагрузки: cos2 6„ ш0 i/Xg 1 - .-cosemax- = o. (зло) Ux 2{xd -xg)2 При найденном значении 6max по формуле (3.9) можно определить значение максимального момента М„ тяу. 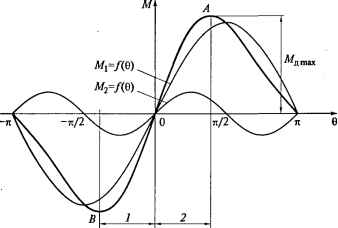 Рис. 3.4. Угловые характеристики привода с синхронным двигателем при постоянных напряжении на статоре и токе возбуждения: 1 - генераторный режим; 2 - двигательный режим 0 ... 18 19 20 21 22 23 24 ... 87 |












