Раздел: Документация
0 ... 19 20 21 22 23 24 25 ... 87 Оценивая результат, надо иметь в виду, что он содержит некоторую погрешность, связанную с пренебрежением активным сопротивлением статорной обмотки. Часто выражение для момента двигателя в абсолютных единицах записывают в виде U,E, - sin6 + -L sin 26 xd2 L L Xg Xj (3.11) где Em - амплитудное значение ЭДС вращения, Ет = Lmdif(a03n. 3.3. Математическое описание синхронного двигателя с демпферной обмоткой Наличие демпферной обмотки существенно усложняет математическое описание двигателя, так как к уже рассмотренной магнитной связи между статорной обмоткой и обмоткой возбуждения добавляются магнитные связи этих обмоток с демпферной обмоткой. Аналогично тому, как это было сделано с обмоткой статора при описании синхронного двигателя во вращающейся системе координат (см. рис. 3.1), демпферную обмотку можно тоже представить в виде двух обмоток, оси которых направлены по осям d и д. При этом должны быть учтены взаимные магнитные связи между статорной обмоткой по оси d, демпферной обмоткой по оси d и обмоткой возбуждения, а также между статорной и демпферной обмотками по оси д. Наличие демпферной обмотки не влияет на уравнения равновесия напряжений (3.1), (3.2) и (3.3), которые могут быть без изменения использованы при описании синхронного двигателя с демпферной обмоткой. К ним должны быть добавлены уравнения равновесия напряжений для демпферной обмотки и выражения для потокосцепления всех пяти фигурирующих в модели обмоток. В абсолютных единицах эти уравне ния записываются так: 0 = RDiD + p4>D; 0 = RQiQ + p4>Q; Wid = LXdhd + Mdfif+ MdDiv; Wig ~ L\qi\g + MqQlQ, 4y= Lfif+ Mfdild+ Mfoio, ЧКд = LDiD + MDdiu + MDfif, где Rd = Rq - активное сопротивление демпферной обмотки; Wp, ¥q, *d> о - потокосцепления и токи демпферной обмотки соответственно; MdD = MDd - коэффициент взаимной индукции между обмоткой статора и демпферной обмоткой по оси d; MqQ = MQq - коэффициент взаимной индукции между обмоткой статора и демпферной обмоткой по оси д; MfD = Mjy - коэффициент взаимной индукции между демпферной обмоткой по оси d и обмоткой возбуждения; LD, Lq - индуктивности демпферной обмотки по осям dug. Для перехода к относительным единицам надо выбрать базовые значения величин, относящихся к демпферной обмотке: базовый ток демпферной обмотки по оси d ID6 - Wi5/MdD; базовый ток демпферной обмотки по оси д Iq5 = Vie/c? базовое потокосцепление демпферной обмотки по оси d базовое потокосцепление демпферной обмотки по оси д Чеб = LqIqz- Значение базового тока демпферной обмотки по оси d выбрано таким, что при протекании его по обмотке создалось бы потокосцепление статорной обмотки по той же оси, равное базовому V/i6. Базовое потокосцепление демпферной обмотки по оси d выбирается равным потокосцеплению, создаваемому базовым током /дб. Аналогичным образом выбраны базовые значения для демпферной обмотки по оси д. Действуя так же, как в подразд. 3.1, можно получить описание электромагнитных процессов в нормированном виде: PWlg 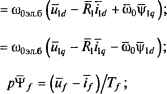 Pd = -h/TD; Px¥Q=-iQ/TQ; / = 4 f-(\-of)xdi\d-\LfiD\ h - У D ~ (1 aD)lf ~ V-Dxdkdi <2 =4Q-(l-oQ)xgilq; Vf= (MpfMdf)/(LfMdD); = (MjyMdpyiLoMdf), где TD, TQ - постоянные времени демпферной обмотки по осям d и q соответственно; (1 - aD), (1 - о0) - коэффициенты связи между статорной и демпферной обмотками по осям d и q соответственно, (1 -a)D = MdD/(LDLid), (1 - oQ) = M2Q/(LQLig); aD, aQ - коэффициенты рассеяния демпферной обмотки по осям d и q соответственно; u./, \x.D - коэффициенты связи между обмоткой возбуждения и демпферной обмоткой по оси d соответственно. Удобная для моделирования в среде MATLAB Simulink нормированная структурная схема электропривода с синхронным двигателем, имеющим демпферную обмотку, во вращающейся системе координат и при питании от источника бесконечной мощности приведена на рис. 3.5. Она может быть использована для расчета переходных процессов, связанных с изменением напряжения и частоты источника питания, момента нагрузки и напряжения возбуждения в пределах, когда эти изменения таковы, что двигатель работает при малых отклонениях значений переменных от их начальных значений, соответствующих синхронному режиму. Это означает, что при расчете переходных процессов в синхронном двигателе на выходах интеграторов, входящих в состав структурной схемы, надо предварительно установить значения УШэн, Чднач, Ф/нач, Фднач, Ф<2нач, Йнач, 6нач, СООТВеТСТВуЮЩИе ВЫб- ранному начальному синхронному режиму. За начальный удобно выбрать режим идеального холостого хода, при котором шнач = со0, бнач = 0- Этим будет обеспечено нулевое начальное значение угла нагрузки. Кроме того, надо иметь в виду, что в установившемся режиме токи в демпферных обмотках отсутствуют, т.е. -= 7д„ач = 0, а напряжение и ток возбуждения в относительных единицах равны друг другу: if -Uf. С учетом этого начальные значения переменных могут быть получены в результате совместного 0 ... 19 20 21 22 23 24 25 ... 87 |












