Раздел: Документация
0 ... 11 12 13 14 15 16 17 ... 87 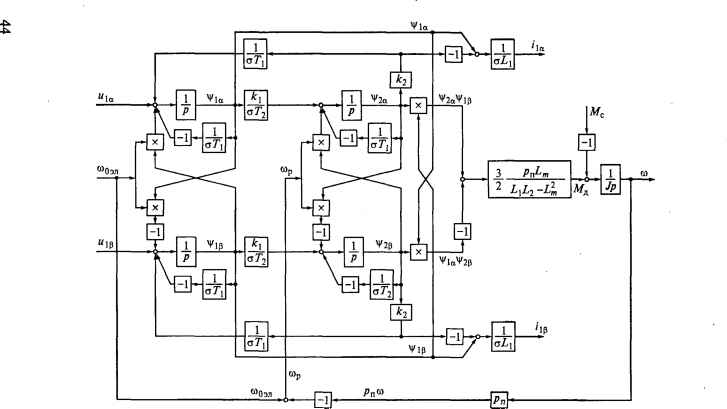 Рис. 2.2. Структурная схема асинхронного двигателя при произвольном повороте вращающейся системы координат относительно пространственных векторов Рис. 2.3. Проекции вектора напряжения статора на оси вращающейся системы координат Р 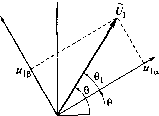 у а Однако в результате описания il- этих переменных пространственны-0х ми векторами, вращающимися вместе с вращающейся системой координат, все переменные и входные воздействия в блоке формирования момента представляют собой сигналы постоянного тока. Эти сигналы остаются неизменными в установившихся режимах и претерпевают изменения при возникновении переходных процессов. При использовании структурной схемы в качестве объекта системы векторного управления, в которой регулирование осуществляется путем изменения частоты с одновременным воздействием на модуль и фазу напряжения на статоре, на вход схемы должны поступать обе проекции вектора напряжения. Если же структурная схема используется для анализа привода с разомкнутой системой регулирования или привода с замкнутой системой регулирования, в которой при изменении частоты изменяется только модуль напряжения, то следует направить ось ос вращающейся системы координат по вектору напряжения статора. При этом £/j = ula, а ы1р = О, чему соответствует равенство углов 6 и 0спри 0] = 0 (см. рис. 2.3). Блок формирования момента включает в себя апериодические звенья, попарно охваченные положительными обратными связями, и четыре перекрестные связи, что предопределяет колебательный характер изменения момента и тока статора. В подразд. 8.1 приведены результаты расчета пуска электропривода с асинхронным двигателем, выполненного в среде MATLAB Simulink по структурной схеме, представленной на рис. 2.2. 2.4. Структурная схема электропривода с асинхронным двигателем при ориентации системы координат по вектору потокосцепления ротора Приведенная в предыдущем подразделе структурная схема (см. рис. 2.2) была построена при произвольном угле поворота системы координат относительно вращающихся вместе с ней пространственных векторов. Это поясняет рис. 2.3, на котором угол 0С представляет собой мгновенное значение угла поворота вращающейся lp\ Рис. 2.4. Неподвижная и вращающаяся системы координат при ориентации оси а по вектору потокосцепления ротора 1а 1 = Ъа ОХ системы координат ос-(3 относительно неподвижной системы координат х-у, а угол 6, - произвольно выбранный угол между осью координат ос и пространственным вектором напряжения на статоре. В установившемся режиме угол 0i остается неизменным. При условии, что ни одна из осей системы координат ос-(3 не совпадает с каким-либо из пространственных векторов, от выбора этого угла зависит только соотношение проекций вектора напряжения на оси координат а и р, а структурная схема при этом остается неизменной. Если напряжение на статоре характеризуется только его модулем, то, как было отмечено в подразд. 2.3, можно принять 0, = 0, в результате чего всегда будет соблюдаться равенство ы1(3 = 0. Но в общем случае, если ось координат ос направляется по одному из пространственных векторов, то это может привести к появлению новой структурной схемы, как это происходит при ориентации оси ос по вектору потокосцепления ротора (рис. 2.4). Рассмотрение этой схемы представляет особый интерес, так как на ее базе строится система векторного управления асинхронным двигателем, имеющая широкое применение в практике электропривода. Для построения такой структурной схемы обратимся к исходной системе уравнений (1.23) для пространственных векторов и исключим из нее векторы потокосцепления статора и тока ротора. Для этого ток ротора из четвертого уравнения системы, определенный как L2 подставим в третье уравнение системы (1.23), определив пото-косцепление статора: У, = I,/, + -/4*2 - LJX) = o-I,/, + №, 2 где c = l-Ll/ (1,12); к2 = LJLb 46 0 ... 11 12 13 14 15 16 17 ... 87 |












