Раздел: Документация
0 ... 10 11 12 13 14 15 16 ... 87 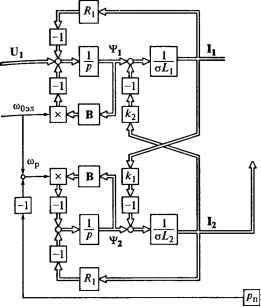
Рис. 2.1. Векторно-матричная структурная схема асинхронного двигателя Векторно-матричная структурная схема асинхронного двигателя представлена на рис. 2.1. Внешними входными воздействиями служат: матрица-столбец статорного напряжения (см. первую формулу из выражений (2.20)), угловая частота статорного напряжения и момент нагрузки Мс. Выходными переменными являются матрицы-столбцы токов статора и ротора, потокосцеплений статора и ротора и токов статора и ротора, а также скорость двигателя со и частота роторной ЭДС сор, зависящая от нагрузки двигателя. 2.3. Структурная схема электропривода с асинхронным двигателем при произвольной ориентации системы координат В предыдущем подразделе математическое описание электропривода с асинхронным двигателем было представлено в виде матрично-векторной структурной схемы. Это удобно, если расчеты ведутся с использованием методов, базирующихся на матричном описании объекта. В других случаях, например при расчетах динамических характеристик привода в среде MATLAB Simulink, предпочтительным оказывается описание двигателя в виде проекций пространственных векторов на оси ос и р или, как их иногда называют, на прямую и квадратурную оси вращающейся системы координат. Относительно этой системы координат было оговорено, что она вращается в электрическом пространстве с той же скоростью со0эл, что и система пространственных векторов, но ничего не было сказано относительно того, как эти две системы ориентированы друг относительно друга. В данном разделе считается, что они могут быть ориентированы по-разному, но так, что каждый из векторов имеет проекцию как на прямую, так и на квадратурную ось. Для построения структурной схемы обратимся к системе уравнений (2.11)...(2.17), подставив в выражения (2.11) и (2.12) значения токов виде формул (2.13) и (2.14), и, таким образом, исключим из первых двух уравнений токи статора и ротора. Кроме того, электромагнитный момент двигателя выразим через пото-косцепления статора и ротора (как в выражении (2.9)). Тогда исходные выражения в пространственных векторах будут иметь вид: Р% =Ui-\r&i- №>) - МэлЪ; аТ2 h =-U*i-№); 2 gl2 где Tlt Т2 - постоянные времени обмоток статора и ротора соответственно, Т\ = Li/Ri и Т2 = LifR2. Подставив в эти формулы выражения для пространственных векторов через их проекции на оси координат и разделив вещественные и мнимые части равенств, получим систему уравнений для построения структурной схемы в виде: 1к2 P¥la = "la--=Г Via + ЩэлЩр + ~ Via, PVip = «1(3 - Юоэл Via - -=Г Vip + -=Г V2p; a7] a/j PV2a A ОТ, Via aft V2a+tOpV2p; fc,1 PV2p = -T Vip - tOPV2a - - V2p5 la =-V(Vla-2V2a); ip =- (vip-V2p); 2a =~-(V2a-fclVla); aZ,2 2p =-7-(v2p -fciVip); 0"Xj2 Ад = tAi -7-(V2aVip - VlaV2p); / <XL2 Юр = ЮОэл - (2.22) Значение модулей векторов тока и потока статора можно рассчитать по формулам: lmax = tJ{L +ip) lmax = (vla + V?p)- Аналогично можно определить и соответствующие роторные величины. Структурная схема асинхронного электродвигателя приведена на рис. 2.2. В ней можно выделить блок формирования электромагнитного момента, входными воздействиями для которого являются проекции вектора напряжения на статоре и1а и и1(3, показанные на рис. 2.3, и частота статорного напряжения со0эл, а выходной величиной - момент двигателя Ма, и блок, описывающий механическую часть электропривода. В простейшем случае второму блоку соответствует основное уравнение механики привода. Его выходной величиной является скорость двигателя. Схема описывает процессы, которые происходят в машине переменного тока, в которой действуют трехфазные переменные величины синусоидальной формы. 0 ... 10 11 12 13 14 15 16 ... 87 |












