Раздел: Документация
0 ... 2 3 4 5 6 7 8 ... 87 Рис. 1.3. Векторная диаграмма асинхронного двигателя в двигательном режиме ление о связи между отдельными переменными в конкретном стационарном 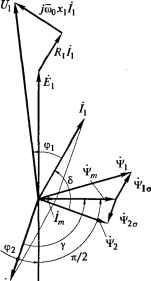 режиме.h Векторная диаграмма для двигательного режима показана на рис. 1.3, где£ по оси абсцисс направлены вектор намагничивающего тока 1т и совпадающий с ним по фазе вектор потокосцепления от магнитного потока в зазоре х¥т = Lmlm. Полные потокосцепления статора х¥1 и ротора 4*2 отличаются от потокосцепления л¥т на величину пото-косцеплений от потоков рассеяния Ц>1с = Zla7, и х¥2а = L2ai2 Вектор ЭДС статора Ёх сдвинут относительно х¥т на угол я/2 в сторону опережения. Вектор ЭДС ротора определяется как Ё2 = -Ё\. Для того чтобы построить вектор напряжения питания, надо учесть, что напряжение превышает ЭДС статора на величину падения напряжения от тока статора в активном сопротивлении и индуктивном сопротивлении рассеяния фазы статора. Значения переменных определяются расчетом по схеме замещения при известном напряжении питания Ux и его частоте, а также при выбранном для построения векторной диаграммы значении относительной частоте роторной ЭДС сор, которая зависит от нагрузки двигателя. Для расчета токов статора и ротора можно воспользоваться выражениями (1.7) и (1.8), записанными в виде: U\={R\+ ]Щ Xi)ii+ j(£>0xmi2; О = УшоХт/, + (со0Д2 /юр + Ую0 х2)12, (1.9) откуда . m0(R2/(up + jx2) £ 1Л(соо,Юр) + уЯ(соо,свр) j ~j(iiOxm у . 2Л(Шо,Юр) + уЯ(ю0,бЗр) - . . со0(Л2/шр+ух2о) -v4(to0,a3p) + yfi(co0,cOp) у4(со0,сбр) и 2?(со0,юр) определяются как: у4(со0,сор) = й0(/с,Л2/(ор - со„ох,х2); В(щ,Шр) = tu0(tu0Xi Д2/юр + х2Д,), где Xi - полное индуктивное сопротивление фазы статора при номинальной частоте; х2 - полное индуктивное сопротивление фазы ротора, приведенной к статору; а - коэффициент рассеяния машины, о = 1 - L2m /(Z,Z2) = 1 - (Xm/Xlx2 )• Рассчитав по формулам (1.9) токи, можно определить ЭДС статора Ei = Ui - ZiCfii +yto0x,a) = Imjxm. 1.4. Представление трехфазной системы пространственными векторами Рассмотренное в подразд. 1.2 математическое описание асинхронного двигателя в виде схемы замещения не учитывает электромагнитных переходных процессов в двигателе. При расчете динамики электропривода с асинхронным двигателем пренебрежение этими процессами может быть допустимым, если они значительно быстрее механических процессов (привод имеет достаточно большой момент инерции). Другой способ описания трехфазных систем базируется на представлении о векторах, ориентированных в электрическом пространстве, т.е. о пространственных (или обобщенных) векторах. В отличие от математического описания асинхронного двигателя в виде схемы замещения для получения векторного описания электромагнитных процессов в асинхронном двигателе надо рассматривать все три фазы трехфазной машины. Кроме того, при представлении трехфазной системы пространственными векторами необ- ходимо учитывать допущения, перечисленные в подразд. 1.1, и, в частности, условие синусоидального характера распределения магнитной индукции по окружности магнитного зазора. Главное магнитное поле статора образуется как сумма пульсирующих главных магнитных полей фазных обмоток, каждое из которых распределено в зазоре по гармоническому закону. Ток в обмотке фазы имеет синусоидальный характер. Поэтому и индукция, и магнитодвижущая сила (МДС) поля фазной обмотки, порожденного этим током, изменяются во времени по гармоническому закону. Приняв /= 0, когда МДС обмотки фазы А имеет максимальное значение, для магнитодвижущих сил обмоток трех фаз можно записать закон изменения их во времени в виде: F\a(*) = AnaxCOS(oW); F\b(?) = Anax COS(С00ЭЛ/ - 2л/3)(1.10) Fib(0 = Fmzx cos(oW - 4п / 3) = тах cos (щэл1 + 2п/3), где fmax - амплитудное значение МДС. Рассмотренные ранее поясняет рис. 1.4, а. На всех графиках ось абсцисс представляет собой развернутую в линию окружность расточки статора (воздушного зазора). Вертикальными линиями отмечены оси обмоток А, В, С. Отложенный по осям абсцисс угол ср представляет собой пространственный угол в эл. рад., отсчитываемый от оси обмотки фазы А. Изображенные сплошными линиями на трех верхних осях косинусоиды показывают пространственное распределение в зазоре магнитодвижущих сил трех фаз в момент времени t = 0 ((%,/ = 0). В соответствии с формулами (1.10) мгновенные значения МДС на осях обмоток будут равны: F\Aif) Lo= Fmw cosO = Fmax; F1B(t) U= Fmax cos(0 -2я/3) = -0,5/w; F1C (0 Uo = Fmw cos (0 + 2к 13) = -0,5Fmax. Эти значения отмечены жирными стрелками по осям обмоток. Зная, что МДС распределены в зазоре по гармоническому закону, по ним можно построить пространственное распределение магнитодвижущих сил в зазоре (ф),=0, Ав(ф)1ыь Ас(фН=о для момента времени t= 0. Результирующая МДС статора /](ф) ,=0, показанная сплошной линией на нижней оси абсцисс, получена как сумма показанных сплошными линиями косинусоид фазных МДС. В другой момент времени амплитуды этих косинусоид будут другими. Если выбрать для следующего рассмотрения момент вре- 0 ... 2 3 4 5 6 7 8 ... 87 |












