Раздел: Документация
0 ... 2 3 4 5 6 7 8 ... 49 X9/YL9 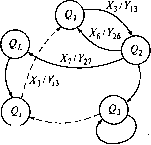 X*IY0. X2/Y32 Рис. 3.4. Граф конечного автомата Граф оказывается более компактным в изображении, чем таблица. В нем отсутствуют повторяющиеся наборы Q[n]. Однако в графе не отражается временной процесс смены состояний КА, который важно знать для управления движением рабочих органов электроприводов. Циклограмма, понятие которой дано в гл. 2, весьма наглядно отражает временной процесс управления, но ценой более громоздкого графического изображения, в котором отражаются все переменные проектируемой ДЛСУ. Однако в синтезе методом типовых узлов необходимость в построении циклограммы возникает при разработке только отдельных узлов, а не всей системы управления. Поэтому при решении вопросов анализа и синтеза ДЛСУ электроприводов предпочтение отдается методу циклограмм. Составленные тем или иным способом таблица, граф или циклограмма для функций переходов и выходов представляют собой соответствующую форму алгоритма КА. Переход от данного алгоритма к его реализации аппаратным или программным способом является сложной задачей. Однако данная задача решается достаточно просто, если перевести алгоритм в аналитическую форму, т. е. в форму структурных формул алгебры логики. Рассмотрим аналитическое представление функций переходов и выходов в дизъюнктивной и конъюнктивной нормальных формах. Из теоремы разложения следует, что любая логическая функция У многих переменных Zi, z2, zm может быть представлена в следующей форме [18]: Y=f(zu z2, zm) = zj(l, z2, zm)+zj(0, z2, Zm). (3.5) Теорема доказывается подстановкой значений Zi = 1 и Z\ = 0 в (3.5). Разложив каждое слагаемое (3.5) последовательно по этой формуле по всем переменным zh получим выражение для функции У: м (3.6) Y = K\f(Z,) + K\f(Z2) + ... + KMf(ZM) = X K)f(Zj), где К) - конституент единицы; f{Zj) - значение функции для у-го набора переменных; j = 1, 2, М; М= 2т; Z\j z\j •zl- zl <• mj 1, где z\j= 1 - единичная форма /-й переменной (zy) в j-м наборе т переменных; z\j = Zy, если Zy = 1, и z\ = Zy, если zy = 0. В выражениях (3.5), (3.6) и в последующих знаки суммирования (+, X), умножения (•) и черта над переменной означают соответственно логические операции дизъюнкции (ИЛИ), конъюнкции (И) и инверсии (отрицания) (НЕ). Среди общего числа наборов М= 2т есть Мх таких, для которых f(Zj) = 1, и М0 таких, для которых f(Z,) = 0. При этом выражение (3.6) можно представить в следующем виде: М,М„ Г = М-1 + 1*]-0.(3.7) Из (3.7) следует дизъюнктивная нормальная форма (ДНФ) представления логической функции: Y = 2ZK)=K\+K\+... + KM(3.8) М т.е. любая логическая функция может быть представлена дизъюнкцией конституентов единицы для тех наборов значений переменных, для которых функция равна единице. Так как второе слагаемое в (3.7) равно нулю, то в ДНФ для набора М0 м„ К) = У и Y = (У) = К{ + К\ + ...+ К1Мо = = К\Кг ...• Кма. -1 Так как Kj = z\jZ2j •...• zmJ = zij + z2J +... + zmJ, то, введя обозначение для нулевой формы /-й переменной ву-ом наборе - z° = = z)j= 0 и для конституента нуля - К*} = К) = z% + Z% + ... + z% = 0, получим так называемую конъюнктивную нормальную форму (КНФ) представления логической функции: м0 i=i т.е. любая логическая функция может быть представлена конъюнкцией конституентов нуля для тех наборов значений переменных, для которых функция равна нулю. Рассмотрим пример математического описания КА. Пусть имеются простейший КА с двумя входами х,, х2 и двумя выходами уи у2 (рис. 3.5), а также хх его таблица переходов и выходов (табл. 3.2). °~ Требуется описать КА графически и анали-тически. У\ = Я У2=Я В данном автомате выходные переменные рис 35 Четырехпо-определяются внутренней переменной состо- люсный конечный яния: yt = q; у2 = q. При числе состояний КА,автомат Таблица 3.2 Таблица переходов и выходов для КА, показанного на рис. 3.5
Примечание. Символ х указывает, что значения не определены. равном четырем, в данном КА используются только три: Хх = 00; Х2 = 10; Хг = 01 (состояние Х4 = 11 запрещено). При одной внутренней переменной q автомат имеет только два состояния: Q, = 0 и Q2=l. Граф данного КА имеет две вершины, определяющие его два разных состояния. Шесть условий смены состояний КА в соответствии с таблицей переходов изображаются в графе направленными дугами (рис. 3.6, а). Циклограмма данного КА, построенная согласно его таблице переходов, наглядно отображает временную последовательность смены состояний автомата в тактах (рис. 3.6, б). Аналитическое описание данного КА выполним в виде структурных формул, пользуясь приведенными выше ДНФ и КНФ. Согласно выражению (3.8) и табл. 3.2 в форме ДНФ можно записать: Ух = q[n] = xxx2q\n -1] + x{x2q[n - 1] + xxx2q[n - 1] = = (X[ + q[n -1] )x2 = xx + x2q[n - 1]. Аналогично согласно выражению (3.9) в форме КНФ можно записать: у, = q[n] = (xl +x2+q[n-l])(xl + х2 + q[n - \})(х1 +х2 +q[n-X\) = = (хх + х2 + q[n - l])(*i + х2) = xl + x2q[n - 1]. Х=00 Х[=00 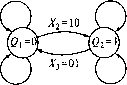
Х3=01Х2 = 10 аб 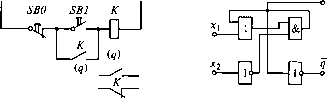 аб Рис. 3.7. Схема реализации триггера на реле (а) и на логическом элементе (б) Таким образом, для заданного КА получено одно и то же аналитическое выражение, по которому легко составить схему практической реализации автомата. При использовании контактных элементов потребуется одно реле Адля выходной переменной q и две кнопки управления SB0 и SB1 для входных переменных (рис. 3.7, а). Бесконтактный вариант КА может быть построен на простейших логических элементах типа И, ИЛИ, НЕ (рис. 3.7, б). Рассмотренный КА представляет собой простой элемент памяти и в бесконтактном исполнении является ЛУ-триггером с входными переменными хх = xs, х2 = хки выходной переменной q[n]=(xs+q[n-l])xR.(3.10) 3.3. Синтез ДЛСУ методом циклограмм Метод циклограмм представляет собой определенную формализацию процедуры синтеза методом типовых узлов. Таблица переходов и выходов, граф, циклограмма - это формы математического описания, формы представления конечного автомата. Задача первой части синтеза - преобразовать технологическое задание на работу электропривода в одну из данных форм алгоритма, по которой составляется завершенный аналитический алгоритм в виде структурных формул. Задача второй части синтеза - перейти к практической реализации полученного алгоритма, выбрав ту или иную элементную базу. В рассматриваемом методе синтеза инструментом формирования алгоритма ДЛСУ выбрана циклограмма, поскольку решается задача автоматизации движения рабочих органов электроприводов в технологическом цикле их работы, что наиболее просто и наглядно описывается циклограммой. Практически оказывается достаточно использовать метод циклограмм для построения не всей ДЛСУ, а лишь ее отдельных наиболее сложных в функциональном отношении узлов. В процедуре данного синтеза выделяются две части: абстрактный синтез - процесс преобразования исходного технологического задания на работу электропривода в завершенный алгоритм конечного автомата в виде структурных формул алгебры логики; структурный синтез - процесс преобразования алгоритма в ДЛСУ на выбранной элементной базе. Поскольку результатом абстрактного синтеза являются структурные формулы, а средством их получения служит циклограмма, то необходимо установить взаимосвязь циклограмм со структурными формулами. Для простейшей циклограммы с одной выходной переменной и одним периодом включения выделим две обобщенные входные переменные: функцию включения S и функцию отключения S" (рис. 3.8, а). Функция S приобретает на включающем такте ДГВ единичное значение (логическая 1) и сохраняет его на всем включающем интервале tB. Функция S" имеет также единичное значение на всем включающем интервале, но обнуляется на отключающем такте At0. Функция S осуществляет включающее воздействие на выходную переменную у, переводя ее из нулевого состояния в единичное. Функция S" осуществляет отключающее воздействие на переменную у, переводя ее из единичного состояния в нулевое. Штриховые линии на рис. 3.8, а означают, что функции включения и отключения могут иметь на указанных интервалах как единичные, так и нулевые значения. Функциями S и S" могут быть как отдельные переменные, так и объединения переменных в дизъюнктивной или конъюнктивной формах. Например, х2 + хх = S, хъхА = S" (рис. 3.8, б). Переменные s Такты -Д/„ 3 4 5 -о х2 *1 *4 аб Рис. 3.8. Функции включения, отключения, временные такты и периоды (а), входные и выходные переменные (б) циклограммы В рассматриваемой циклограмме у = 1 только на одном периоде - периоде включения tB, когда S = 1 и S" = 1. На всех других устойчивых тактах у = 0. Тогда, согласно ДНФ (3.8), для функции Y имеем структурную формулу Y=SS".(3.11) Если циклограмма для У имеет п периодов включения, то Y = ±SISI(3.12) /=1 где Sj S" - функции включения и отключения на /-м периоде включения. Циклограмма, отражающая операцию задержки времени, приведена на рис. 3.9. При задержке времени на включение /В1СЛ (см. рис. 3.9, а) Y=SS"[+tBKJ,(3.13) при задержке времени на отключение /откл (см. рис. 3.9, б) Y=SS"[+t0TKJI].(3.14) Итак, имея циклограмму ДЛСУ, можно получить описывающие ее структурные формулы, являющиеся алгоритмом управления. По структурным формулам можно составить принципиальную схему ДЛСУ. Выделим этапы синтеза методом циклограмм в составе его двух частей. 1.Составление исходной циклограммы по технологическому заданию на движение электропривода. 2.Преобразование исходной циклограммы в реализуемую циклограмму. 3.Составление структурных формул по реализуемой циклограмме. 4.Выбор элементной базы для ДЛСУ. s s" Рис. 3.9. Циклограммы, отражающие операции задержки времени на включение (а) и отключение (б) 0 ... 2 3 4 5 6 7 8 ... 49 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||












