Раздел: Документация

0 ... 19 20 21 22 23 24 25 ... 162

дена. А это в свою очередь равносильно наличию ненулевого решения а однородной системы (£ -А)а=&, т. е. а = Аа~. В этом случае Х= 1 - собственное значение матрицы А, однако по теореме 9.3 ее собственные значения меньше 1. Осталось предположить, что А-продуктивная матрица, но для матрицы £ - А существует обратная матрица, среди элементов которой встречаются отрицательные. Пусть atk - один из них, а у - вектор-столбец из R", к-я координата которого равна I, а остальные координаты равны нулю. Тогда ввиду продуктивности А существует неотрицательный вектор-столбец х такой, что Ах+у=х. Отсюда у=(Е-А)Х,

(Е-А)-у=(Е-А)?Е-А)х = х. "Но /-я координата в (Е-А)~ у равна я,*, что

противоречит неравенству х > 0 . Следствие доказано.

Т9.1. Доказать следствие 9.1.

Т9.2. Доказать, что если а - собственный вектор некоторой матрицы, то и вектор ка, где любое, не равное нулю число, также является собственным вектором, соответствующим тому же собственному значению, что и

Т9.3. Доказать, что система векторов, состоящая из собственных векторов, соответствующих попарно различным собственным значениям некоторой матрицы является линейно независимой.

Т9.4. Известно следующее свойство определителя: для любых двух квадратных матриц С, В одного порядка \СВ\ = \С\\В\. Пользуясь этим свойством, доказать, что собственные значения обратной матрицы равны обратным величинам для собственных значений матрицы А,

Т9.5. Доказать: нуль является собственным значением квадратной матрицы Л, если и только если А вырождена.

Пусть А - положительная квадратная матрица. Тогда любой ее неотрицательный собственный вектор является положительным и соответствует максимальному собственному значению ХА матрицы А.

Пусть А положительная квадратная матрица. Тогда любые два ее положительных собственных вектора О и Ь линейно зависимы, т. е.~5=оТ йдля некоторого положительного числа а.

В задачахдля данной матрицы А найти все ее собственные значения и

собственные векторы, им соответствующие.

Задачи

для самостоятельного решения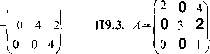

(А 2 И

П9.2. А

П9.4. Л =

П9.7.Л =

Г1 о (Г 3 2 0

0 3 5)

Г4 5 7 0 4 6 О 0 1

П9.10. А--

(\ о о 6)

0 10 0

0 0 1 о

П9.13. А<=

П9.16.Л :

П9А9. А=

			°)

П9.5. А --

0 0 20

0 0 02

П9.8. А=

(Л 87 О 4 1

0 0 4

П9.11.

П9Л4. А=

(\ I 42 0 2 2 1

0 0 33

1,0 О О4

[2 0 0<Л

5 2 00

4 6 30

П9.17.А =

(2 1 Ол

О 2 1 0 0 2

П9.6.

П9.9.

"1

П9.12.

(\ о о 01 1 20 0

12 3 0

4 2 3 4

П9.15.Л =

П9.18. А =

П9.20. Л =

ГэззО

0333

0033

0003,

П9.21. А=

Ответы,указания) решения

Т9.1. Указание: воспользоваться равенством \А\~~ \AJ\.

Т9.2. Утверждение непосредственно проверяется по определению.

Т9.3. Докажем индукцией относительно числа векторов в системе. Для одного вектора утверждение следует из задачи Т2.1. Предположим, что утверждение верно для систем с к-1 векторами. Пусть Я, Хг, Хк - попарно различные собственные зна-

чения матрицы А, a,, а 2, а, - собственные векторы, им соответствующие. Если система векторовлинейно зависима, то нулевой вектор представим в

виде ненулевой комбинации этих векторов: ~ЬТ = afar, +... +vTkakУмножим обе части этого равенства слева на матрицу А -

(А -А.£)От=а,(Ля,- + а2(А а2~Ха, ) +... + ак{Аак-Х~ак)

5Т = а,(Л, 5,-Х.Т а, ) + о2(Х2яг)1аг)+ ...а-йД От = аз(Х2-Х)а! + а3(>.з->,)й,+ ... +404-

Так как по индуктивному предположению система векторов... , линейно

независима, то из последнего равенства следует, что все коэффициенты а2(Х2 - -i), а(Хз - Х]),а*(А ~ Я.)равны нулю. Но тогда =."= &k= 0, ибо все числа X2-Xiy h-h,отличны от нуля. Следовательно, 0т=а,5,,т.е. а, -0. Получено

противоречие, поскольку рассмотренная комбинация векторов ненулевая.

Поскольку предполагается, что обратная матрица существует, то матрица А не имеет нулевого собственного значения (см. задачу Т9.5 и следствие 6.2). Предположим, что а - собственное значение матрицы А. Это равносильно равенству \А~аЕ\ = 0 (теорема 9.1). Разделив каждую строку матрицы А - аЕка а получим

равенство \-А -Е = 0. Теперь умножим обе части этого равенства на /Г: а

аааа

И, опять таки, по теореме 9.1 последнее равенство равносильно тому, что---соб-

ственное значение матрицы Утверждение доказано. Т9.5. Указание: воспользоваться следствием 5.3.

Т9.6. Согласно теореме 9.2 и следствию 9.1, существует положительный вектор а, такой что ATa=KAa .Пусть теперь b - произвольный неотрицательный собственный вектор матрицы, т. е. Ab = ее А для некоторого собственного значения а, Если /-я координата в b равна нулю, то произведение строки матрицы А на b было бы равно нулю, что невозможно ввиду А, > 0, b >0 и b * 0т . Поэтому

b - положительный собственный вектор. Применяя теорему 1.1 и утверждение

задачи Т3.5, с одной стороны, имеем:

\У (АЬУ] = [5Т bTAT][a7A-bt] = [(A15y .ЬТ] = ХА[5Т -Ьт].

0 ... 19 20 21 22 23 24 25 ... 162