Раздел: Документация
0 ... 41 42 43 44 45 46 47 ... 143 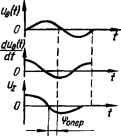 по фазе у. Причиной этому является вносимое инерционными звеньями системы запаздывание колебаний по фазе, которое, как видно из выражения для ЛФЧХ, яр (со) = —л/2 — arctg аТг — arctg <аТ2 и самой характеристики ф (со) возрастает с увеличением частоты. На некоторой частоте соя запаздывание колебаний на выходе системы относительно колебаний на его входе становится равным 180°, когда отрицательная обратная связь превращается в положительную и удовлетворяется условие самовозбужде- Рис. 5.4. Получение ния системы по фазе.опережения по фазе. Таким образом, ухудшение переходного процесса и потеря устойчивости при увеличении kp системы связаны с наличием запаздывания в системе колебаний по фазе. Отсюда нетрудно ответить на поставленный выше вопрос: чтобы при увеличении /гр система осталась устойчивой и обеспечивался требуемый запас устойчивости по фазе у и амплитуде а, необходимо частично скомпенсировать запаздывание в некоторой полосе частот, расположенной около частоты среза сос2, соответствующей повышенному коэффициенту усиления kp2 системы, и тем самым деформировать ЛФЧХ системы, приподняв ее верх, как, например, показано пунктирной кривой на рис. 5.3. Такую деформацию ЛФЧХ можно осуществить включением последовательно элементам системы устройства, которое бы в отличие от других элементов системы вносило не запаздывание, а опережение по фазе синусоидальных колебаний в указанной выше полосе частот. Опережение по фазе фопер может быть достигнуто в результате сложения напряжения сигнала рассогласования Me (f) с производной от него due (f)ldt (рис. 5.4). Такое сложение осуществляется с помощью дифференцирующего фа-зоопережающего устройства, которое будет рассмотрено ниже. Таким образом, одним из способов улучшения показателей качества системы является введение производной от сигнала рассогласования в алгоритм управления. Возможность коррекции с помощью производной от сигнала рассогласования была рассмотрена с помощью частотных характеристик. Выясним теперь физический смысл введения производной от сигнала рассогласования в алгоритм управления во временной области. Физический смысл введения производных от сигнала рассогласования в алгоритм управления I Предположим, что сигнал рассогласования системы «е (0 изменяется по кривой / (рис. 5.5). Изменение производной от сигнала рассогласования изображено кривой 2. Если система реагирует только на сигнал рассогласования «е (t), то вследствие того, что сигнал при прохождении через инерционные элементы запаздывает и чувствительность исполнительного элемента, например двигателя, конечна, система начинает отрабатывать ошибку рассогласования не сразу, а че-резнекоторое время после ее появления. Если же на исполнительный 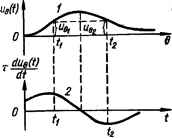 Рис. 5.5. К физическому смыслу введения производной от сигнала ошибки в алгоритм управления. двигатель системы будет поступать и производная, то последний начнет отрабатывать ошибку значительно раньше и быстрее, поскольку производная при малом сигнале рассогласования (в момент его появления) может иметь конечное значение. Если система реагирует на сигнал рассогласования «е (0, то вращающий момент двигателя системы одинаков как в момент времени tx, когда сигнал рассогла- • сования растет, так и в момент t2, когда он убывает. Между тем, было бы жела- . тельно, чтобы в момент tx двигатель развивал больший вращающий момент Мвр для более эффективного противодействия нежелательному возрастанию ошибки, а в момент t2 — меньший Мвр для предупреждения перерегулирования, т. е. возможного перехода системы по инерции через равновесное состояние. Такое изменение Мвр достигается введением производной в алгоритм управления. В этом случае Мвр двигателя в момент времени tx увеличивается, поскольку воздействия от щ> (t) и %due {t)ldt совпадают по знаку, • а в момент t2 уменьшается или даже изменяет свое направление, так как воздействия от щ (t) и xdue (t)/dt противоположны по знаку. В результате такого изменения вращающего момента двигателя за счет введения производной в алгоритм управления уменьшается максимальное значение ошибки, уменьшается или даже устраняется перерегулирование, переходный процесс системы затухает быстрее. Реагируя на производную, система как бы чувствует не только ошибку, но и тенденцию ее дальнейшего изменения. На этом основании управление по производной иногда называют управлением с предварением или опережением. Показанная на рис. 5.3 деформация ЛФЧХ, соответствующая введению в алгоритм управления производной от сигнала рассогласования с помощью фазоопережающего устройства, является не единственно возможной. Как будет показано ниже, улучшение показателей качества системы может быть достигнуто и при отличных от рис. 5.3 деформациях ЛЧХ системы, соответствующих другим изменениям алгоритма управления, реализуемых с помощью иных корректирующих устройств. В общем случае выходной сигнал корректирующего устройства, кроме составляющей, пропорциональной входному сигналу (сигналу рассогласования), может содержать составляющую, пропорциональную некоторой функции от входного сигнала, например производной, интегралу во времени, их сумме. Необходимое функциональное преобразование сигнала рассогласования системы может быть достигнуто с помощью корректирующих устройств, включаемых либо последовательно элементам системы в главный контур управления, либо в местные обратные связи, охватывающие часть элементов системы. В соответствии с этим корректирующие устройства называются последовательными и параллельными.. На практике встречаются случаи, когда коррекция САУ осуществляется с помощью включения как последовательных, так и параллельных корректирующих устройств одновременно. 5.2. Коррекция САУ с помощью последовательных дифференцирующих фазоопереэкающих устройств постоянного тока Дифференцирующий фазоопережающий ЯС-контур постоянного тока. Передаточная функция и частотные характеристики контура Как уже отмечалось, опережение по фазе синусоидальных колебаний, необходимое при коррекции САУ, достигается с помощью дифференцирующих фазоопережающих устройств. Одним из распространенных таких устройств является дифференцирующий /?С-контур постоянного тока (рис. 5.6, а). Для определения передаточной функции контура составим уравнения напряжения этого контура в операционной форме: 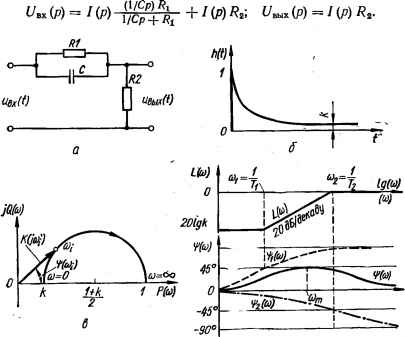 г Рис. 5.6. Дифференцирующий фазоопережаюший ЯС-контур и его характеристики: а — схема; б — переходная функция; в ™= АФЧХ; г — ЛЧХ, 0 ... 41 42 43 44 45 46 47 ... 143 |












