Раздел: Документация
0 ... 42 43 44 45 46 47 48 ... 143 Из второго уравнения находим / (р) = с7вь,х (рУКц и, подставляя в первое уравнение, получаем с7вх(р) = [RAR2 + CPR&) + 1] Um(p). После преобразования откуда передаточная функция контура или Kip) = UBVX(p)/UBK(p) = k(TlP + l)/(T2p + 1),(5.3) где 7\ = i?xC — постоянная времени контура по производной; k = = RJiRi + R2) — коэффициент усиления контура по сигнальной составляющей; Т2 — kTx — постоянная времени отставания. Поскольку k < 1, то Т2 < Тх. Из формулы (5.3) можно определить изображение переходной функции контура Н \р), подставив с7вх (/?) = 1/р: H(p) = k(TlP+1)1(7+1) р. Кривая переходной функции контура h (t) изображена на рис. 5.6, б. Комплексная передаточная функция контура К (/со) = k (Ti;co + 1)/(Г2/со + 1).(5.4) АФЧХ контура, построенная на основании выражения для К О40)» показана на рис. 5.6, е. Из рисунка видно, что АФЧХ контура представляет полуокружность, расположённую в первом квадранте. ЛЧХ контура изображены на рис. 5.6, г. ЛАЧХ L (со) контура построена в соответствии с выражением L(co) = 20 Igk + 20 IgV 7V+1 — 20 lg V TV + 1 , (5.5) а ЛФЧХ гр (<o) контура на основании формулы г]з (со) = arctg со7\ — arctg соГ2.(5.6) - Логарифмические ФЧХ, соответствующие первому и второму слагаемым выражения (5.6), изображены на рис. 5.6, г кривыми % (со) и г]з2 (со). Как видно из выражений (5.4) и (5.6), а также из ЛФЧХ % (со) и г]з2 (со), член (7\/со + 1), стоящий в числителе комплексной передаточной функции (5.4) контура, обусловливает опережение, рав- : ное arctgcoT1!, а член (Г2/со + 1), находящийся в знаменателе, определяет запаздывание, равное arctgcoTV Опережение возможно в случае, если постоянная времени производной (опережения) Тг контура больше, чем постоянная времени отставания Т2. Поскольку в дифференци- рующем контуре это условие выполняется, то, как видно из АФЧХ и ЛЧХ контура (рис. 5.6, в, г), последний создает опережение по фазе синусоидального сигнала в определенной полосе частот. Физически опережение можно объяснить сложением на резисторе R2 напряжения их (t) = kuBX (t), пропорционального ивх (t), выделяющегося на R2, как на элементе делителя, образованного резисторами R1 и R2, и напряжения щ (г) = iduByi (f)ldt, приближенно пропорционального производной от ивх (г), выделяющегося на R2, как элементе дифференцирующей цепочки R2C. Найдем частоту com, при которой контур создает максимальный угол опережения ipmax. Для этого необходимо взять производную dip (to)/dco, приравнять ее нулю и из полученного таким образом уравнения определить сот. В соответствии с выражением (5.6) игр(co)/dco = 7УП + (com7\)3] - T2/[l + (со2] = О, откуда ©m = l/W, = Уй* = 1 /VТ\Ь = l/i Vk ,(6.7) т. е. сот равна среднему геометрическому значению частот сопряжения ее»! и со2. Максимальное значение угла опережения г]зтах найдем, подставив значение со,„ и выражение (5.6): г>тах = arctgl/T-i/T,— arctg ]/7у7\, т. е. чтобы получить большее значение максимального угла опережения, необходимо брать постоянные времени опережения Тг и отставания Т2, как можно больше отличающимися друг от друга. Учитывая, что Тг и Tz связаны через коэффициент усиления k дтюшением TJT2 = Ilk, выражение для гртах может быть записано в следующем виде: 4W = arctg (l/Vk) — arctg Vk,(5.8) т. е. для получения большого угла опережения следует уменьшить коэффициент усиления контура. Рис. 5.7 иллюстрирует изменение г]зтах за счет изменения Тг и k при Т2 = const, а рис. 5.8 — за счет изменения 7*2 и k при Тг — const. На обоих рисунках соответствующие ЛАЧХ и ЛФЧХ обозначены одинаковыми цифрами. Возможно также одновременное изменение Tlt Tz и k. дБ 20lgk{ J V f ± Тг --- u> I ki>/t2 T2= const 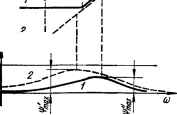 Щкг\---- 4>(u)\ 90° О Рнс. 5.7. Изменение гр, за счет Тх и k при г2 = const. дБ О 20tgk, 201дкг m SO0 if ± Тг Ms 1 A- v £V П>т{ ki>kz Tt=const
Рис. 5.8. Изменение контура за счет Т2 и k при 7"i = const. Рис. 5.9. Функциональная схема системы, скорректированной последовательным дифференцирующим фазоопережающим ЯС-контуром постоянного то- Д ка.- Дифференцирующий #С-контур постоянного тока выгодно включать в САУ, у которой элемент сравнения преобразует отклонение управляемой величины от заданного значения в напряжение постоянного тока, а в качестве усилителя используется усилитель с входом на постоянном токе (например, электронный, магнитный, электромашинный). В качестве примера на рис. 5.9 изображена функциональная схема следящей системы, стабилизированной последовательным дифференцирующим /?С-контуром постоянного тока ДК. В этой системе элементом сравнения служит потенциометрический мост П, питаемый постоянным напряжением, в качестве усилителя применен усилитель постоянного тока УПТ, а исполнителем является двигатель постоянного тока М. Выбор параметров дифференцирующего фазоопережающего RC -контура. Возможности улучшения показателей качества САУ с помощью контура Задачу выбора параметров контура, применяемого в качестве последовательного корректирующего устройства САУ, и возможности улучшения показателей качества с помощью этого контура рассмотрим на примере коррекции следящей системы (см. рис. 5.9). Пусть КПФ нескорректированной системы в разомкнутом состоянии Кр (/со) = VIU + m (1 + m /со], V = Т2/Тх = 0,27. (5.9) Примем следующую методику решения задачи. Построим ЛАЧХ нескорректированной системы с заданным запасом устойчивости по фазе у = Yi, выберем оптимальные в том или ином смысле параметры корректирующего контура, построим ЛАЧХ скорректированной системы при том же запасе устойчивости ух. Определим, во сколько раз удается с помощью контура повысить коэффициент усиления kp, частоту среза сос системы, а следовательно, уменьшить динамическую ошибку и время регулирования системы. Пусть необходимый запас устойчивости по фазе у = 30°. С помощью графиков у = f (V) (см. рис. 5.2) находим для V = 0,27 частоту среза сос системы, при которой обеспечивается у = 30°: сос = 1/7\. ЛАЧХ L (со) и ЛФЧХ ф (со) нескорректированной системы, КПФ которой определяется выражением (5.9), а частота среза сос = \1ТХ, изображены на рис. 5.10. Из рисунка видно, что коэффициент усиления системы 0 ... 42 43 44 45 46 47 48 ... 143 |












