Раздел: Документация
0 ... 44 45 46 47 48 49 50 ... 143 Достоинства и недостатки коррекции САУ с помощью последовательных дифференцирующих фазоопережающих устройств. Из изложенного выше видно, что достоинство коррекции САУ с помощью последовательных дифференцирующих фазоопережающих устройств (путем введения производных в алгоритм управления) состоит в том, что одновременно с увеличением коэффициента усиления kp системы удается увеличить и ее частоту среза сос, т. е. наряду с уменьшением ошибки системы в установившемся режиме имеется возможность уменьшить и время переходного процесса. Можно отметить недостатки коррекции САУ путем включения последовательных дифференцирующих фазоопережающих устройств. Последние вносят значительное ослабление в области низких частот, т. е. в области существенных частот спектра полезного сигнала. Это ослабление тем интенсивнее, чем большее опережение должно обеспечить фазоопережающее устройство. Для компенсации этого ослабления необходимо увеличивать коэффициент усиления системы за счет других ее элементов. Высокие частоты фазоопережающее устройство пропускает без ослабления. Поэтому, если на полезный сигнал, подлежащий дифференцированию, накладываются быстроизменяющиеся шумы или помехи, спектр которых расположен в области высоких частот, то эти шумы и помехи будут пропускаться устройством без ослабления. Существенное ослабление полезного сигнала, с одной стороны, и пропускание без изменения помех, с другой, приводят к уменьшению отношения сигнала к шуму, что является причиной увеличения динамических ошибок системы. 5.3. Коррекция САУ с помощью последовательных интегрирующих устройств При коррекции САУ с помощью последовательных дифференцирующих устройств с увеличением коэффициента усиления системы увеличивается и частота среза сос. При отсутствии помех, действующих на вход системы, это способствует улучшению показателей качества системы: с увеличением коэффициента усиления системы уменьшается установившаяся ошибка, а увеличение частоты среза приводит к уменьшению времени регулирования. Однако если вместе с задающим воздействием на систему поступают помехи, то дифференцирующий контур, как правило, не дает желаемых результатов. В этом случае система должна удовлетворительно пропускать сигнал и наиболее эффективно подавлять помехи. Задающее воздействие обычно представляет собой медленно изменяющуюся функцию времени и поэтому его частотный спектр является узким, расположенным в области низких частот. Помехи же изменяются быстрее во времени, поэтому имеют более высокочастотный спектр, чем задающее воздействие. Следователь-1 о, для получения минимальных ошибок при наличии помех система должна иметь узкую полосу пропускания в области низких частот (малую частоту среза) и возможно большой коэффициент усиления. 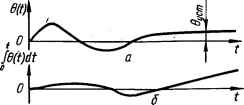 Рис. 5.11. Кривые изменения сигнала ошибки (а) и ее интеграла (б). С точки зрения уменьшения уровня шумовых помех систему целесообразно корректировать не дифференцирующим, а интегрирующим контуром, который, как будет показано ниже, позволяет увеличивать коэффициент усиления системы, не увеличивая ее частоты среза. С помощью интегрирующего контура целесообразно осуществлять коррекцию также тех систем, от которых требуется большой коэффициент усиления (высокая динамическая точность). Выясним физический смысл введения интеграла от сигнала рассогласования в алгоритм управления. Если на исполнительный двигатель системы поступает напряжение, пропорциональное сигналу ошибки в (t) (рис. 5.11, а), то при изменении задающего воздействия с постоянной скоростью, как известно, возникает скоростная ошибка 0уст (t). Если же напряжение ошибки предварительно подавать на интегрирующее устройство, а затем с его выхода — на исполнительный двигатель, то скоростная ошибка будет уменьшаться. Это можно объяснить тем, что напряжение на выходе t> интегратора j %{t)dt (рис. 5.11, б) будет увеличиваться до тех пор, о пока не достигнет значения, при котором скорость изменения управляемой величины не будет равна скорости изменения задающего воздействия, а скоростная ошибка не станет равной нулю. Уменьшения до нуля скоростной ошибки можно достичь включением в систему интегрирующего устройства, близкого к идеальному, например, дополнительного двигателя, угол поворота которого приближенно равен интегралу от входного напряжения. Здесь реализуется случай повышения порядка астатизма системы на единицу. Если же в систему включить пассивную интегрирующую цепь, выходное напряжение которой не может расти до бесконечности, то установившаяся ошибка полностью не устраняется, но существенно уменьшается. Порядок астатизма системы при этом остается прежним, Как видно из рис. 5.11, интегральная кривая запаздывает относительно кривой изменения сигнала ошибки в переходном режиме, что приводит к ухудшению переходного процесса системы. Интегрирующий R С -контур постоянного тока. Передаточная функция и частотные характеристики контура Наиболее распространенным контуром является интегрирующий С-контур постоянного тока, схема которого изображена на рис. 5.12, а. Для определения передаточной функции контура запишем Уравнения напряжения контура: Ui (р) = + i/Ср + i (р); иш (р) = (мер + /?о / (р). 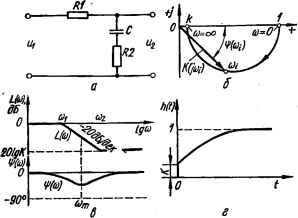 Рис. 5.12. Интегрирующий /?С-контур постоянного тока и его характеристики: а — схемы контура; б — АФЧХ; е — ЛЧХ; г — переходная функция. Подставив значение / (р) из второго уравнения в первое, получим Ui (Р) = (fli + Я. + 1/Ср) [1/(1/Ср + RJ] U% (р), отсюда находим передаточную функцию контура или /Ш =(?>+!)/(?>+1),(5.14) где Т2 = С/?2 — постоянная времени опережения; Тг = С (Rt + + R2) — постоянная времени отставания. Соотношение между Тг и Т2 таково: Т2/Тх — R2I(RX + R2) = k, т. e, T2 = Txk. Поскольку k < 1, то T2 > Т2. Комплексная передаточная функция контура Я (/со) = (72/со + 1)/(7усо +1).(5.15) АФЧХ контура (рис. 5.12, б), построенная на основании выражения (5.15), представляет собой полуокружность, расположенную в четвертом квадранте. ЛАЧХ контура L (со) (рис. 5.12, в) построена в соответствии с выражением L(co) = — 20\gV TV + 1 + 20\gV 7V + 1 . В области низких (со % = 1/Тг) и высоких (со !>со2 = 1/Т2) частот выражения для ЛАЧХ имеют соответственно вид: LH.4(co) = 0; Lb.4(co) = — 20 Igor! + 20 \gaTM = 20\gk. ЛФЧХ контура гр (со) (рис. 5.12, в) построена в соответствии с выражением ip (со) = —arcig + arctg соТ2. 0 ... 44 45 46 47 48 49 50 ... 143 |












