Раздел: Документация

0 ... 20 21 22 23 24 25 26 ... 49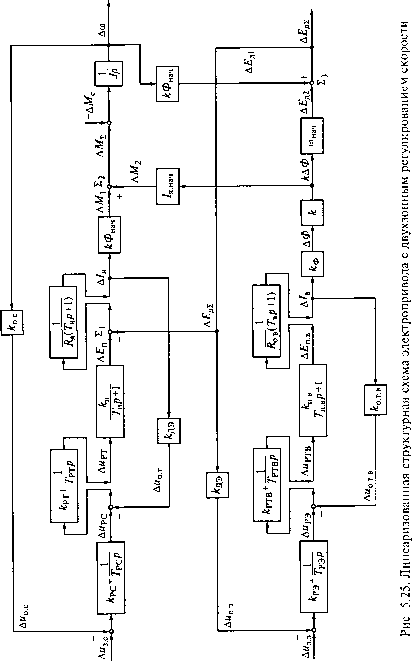

С учетом малости произведений Д/яДФи ДсоДФ значения AMZ и Д-ЕдЕ на рис. 5.25 отражены суммами их составляющих:

ДМ2 = АМ\ + АМ2 = &ФначД/я + Л.начА:ДФ;

Д£д2: = Д£д1 + Д£д2 = кФначА(а + соначМФ.

Часто, особенно для двигателей с шихтованными станинами, когда ТВ1 <к Тв, влиянием вихревых токов на отклонение магнитного потока пренебрегают. Тогда (при Гвт = 0) передаточная функция силовой цепи обмотки возбуждения двигателя как объекта регулирования с выходом по току возбуждения определится (см. рис. 5.25) следующим образом:

W (;;) А/в( -

олКР) Аи„в(р) ЯЛТ„.вр + ЩТвр + 1У

Отсюда при выборе передаточной функции разомкнутого КТВ с учетом коэффициента котв в виде

Wp) = к0Т.вавТр(Твр + 1У

передаточная функция регулятора тока возбуждения определится как

Иргв(/») = *ртв + т 1 ,

1 PTB/7

где ав - соотношение постоянных времени КТВ при его настройке на модульный оптимум, ав = 2...4; к?тв - коэффициент передачи пропорциональной части PTB, &РТВ = TB/TpjB; Т?тв - постоянная времени интегрирования ПИ-регулятора РТВ, 7рХВ = к k

"о.т.вап.в г

~ R в -в*

При выбранном регуляторе РТВ передаточная функция замкнутого КТВ

А1в(р) 1

"КР) ДирЭ() к0,л[авТаяр(ТплР + 1) + 1У

Синтез регулятора ЭДС полезно предварить оценкой степени влияния на ток якоря составляющих суммарного отклонения ЭДС двигателя АЕл2 (рис. 5.26), вызванного при постоянстве скорости двигателя изменением лишь магнитного потока двигателя. С этой целью переменная АМ2 из сумматора Х2(см. рис. 5.25) переносится на сумматор Ц, (см. рис. 5.26), где результат ее переноса

Д/±д2 = Д Ф/я.начД,( 7> + 1)/Фнач

с противоположным знаком суммируется с составляющей АЕя2 = = соначААФ. Составляющая АЕ& обусловлена изменением жесткости

---

-f АД

д2Е

1

BJLT.PH)

А/,

ае,

Д2

д2

/Я.начД,(+1)

Рис. 5.26. Узел воздействия потока на ЭДС двигателя

механической характеристики двигателя при изменении его потока. При скорости выше номинальной (сонач> соном), когда вступает в действие контур регулирования ЭДС и имеет место отклонение ДФ, эта составляющая намного меньше составляющей Д£д2, связанной с изменением начальной скорости двигателя. Поэтому при сонач > соном влиянием АЕ& на ток якоря можно пренебречь. Тогда при исключении в структурной схеме рис. 5.25 связи между АМ2 и ДФ передаточная функция объекта регулирования ЭДС двигателя при постоянстве его скорости (Дсо = 0) определится как

ц/ (п\ = АЕр) = ккф(йнгч ккфанач

°*зКР) АиРЭ(р) к0.тл[авТплр(Тплр + 1) + 1] - к0,л(авТплр + 1)"

Тогда с учетом обратной связи по ЭДС двигателя передаточная функция регулятора ЭДС

WP3(p) = 7fJ-.

Здесь 7рЭ - постоянная времени интегрирования регулятора РЭ;

7рэ = яэавАдэ ккф(£>нзчТп ,в/котв,

где аэ = 2..А - соотношение постоянных времени КЭ при его настройке на модульный оптимум.

Таким образом, при подобной настройке и без учета влияния вихревых токов в магнитопроводе двигателя применяется интегрирующий регулятор РЭ. При этом передаточная функция замкнутого КЭ

узшэ(р) = аем= - •

Аизэ(р) каэ[аэавТпвр(авТплр + 1) + \]

Поскольку из-за нелинейности характеристики намагничивания двигателя значение А:фсонач при изменении магнитного потока меняется в пределах

где кфтш(от!1Х соответствуют минимальному, а &фтахсотщ - максимальному значениям магнитного потока, то при выборе параметров регулятора РЭ принимают &фСонач = Amaxcomin. Тогда условие устойчивости замкнутого контура регулирования ЭДС будет сохраняться и при уменьшении £фСонач.

Для обеспечения устойчивости замкнутого КС во всем диапазоне изменения кФтч параметры регулятора РС определяют при максимальном значении &Фнач = кФнои.

Статические электромеханическая и механическая характеристики электропривода с двухзонным регулированием скорости могут быть определены по структурной схеме рис. 5.25 при /> = 0. Для ПИ-регулятора тока и И-регулятора ЭДС двигателя электромеханические и механические характеристики электропривода при П и ПИ-регуляторах скорости приведены на рис. 5.27. При h < Л max ПИ-регулятор скорости обеспечивает астатизм регулирования скорости от нуля до ютах (линии 1). При П-регуляторе скорости электромеханическая и механическая характеристики электропривода имеют конечное значение жесткости (линии 5). При 1Я = 1ятзх, значение которого задается уровнем ограничения выходного напряжения БО, система обеспечивает за счет ПИ-регулятора тока якоря его постоянство во всем диапазоне изменения скорости. Максимальный же момент двигателя Мтгх = кФН0Ы1ятт сохраняется постоянным лишь при со < со„ом, а затем снижается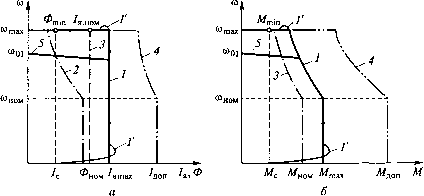

Рис. 5.27. Электромеханическая (а) и механическая (б) характеристики электропривода и фазовые траектории со(7), со(Ж) при пуске двигателя

при /ятах= const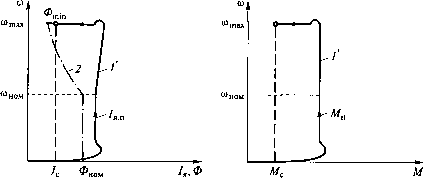

---

Рис. 5.28. Фазовые траектории со(/) (а) и со(А/) (сТ) с линейно нарастающим заданием скорости

до Mmin пропорционально уменьшению магнитного потока двигателя с номинального Фном до Фтт (линия 2). Длительно допустимому по нагреву двигателя режиму работы электропривода при h = Л.ном соответствуют линии 3, а кратковременным допустимым перегрузкам по току (7я.до„) и моменту (Мтп) двигателя - линии 4.

Фазовые траектории со(/я) и со(М) при пуске двигателя с постоянной статической нагрузкой (Мс = const) в режиме поддержания постоянства тока якоря на уровне /ятах < /до„ (в режиме ограничения выходного напряжения БО) отличаются от статических характеристик лишь в начале и по окончании пускового режима (линии Г на рис. 5.27). При этом до момента достижения номинальной скорости двигатель разгоняется с постоянным ускорением, определяемым динамическим моментом Мдин = Мтт - Мс, а при со > соном за счет уменьшения Мтн темп разгона двигателя снижается. После достижения заданного значения скорости разгон двигателя прекращается и ток двигателя устанавливается равным /с = Мс/(кФтЫ).

Если пуск двигателя осуществляется от задающего устройства с линейно нарастающим напряжением задания скорости и при этом пусковой ток якоря 1ЯП не превышает /ятах, то при Мс = const момент двигателя во время разгона остается практически постоянным и равным М„ = Л/с + Мтн во всем диапазоне регулирования скорости (линия Г на рис. 5.28, б). В начале и по окончании переходного процесса возможны лишь перерегулирования момента в соответствии с динамическим перерегулированием тока якоря. Постоянство пускового тока сохраняется только до номинальной скорости, после чего по мере снижения потока (линия 2) ток якоря возрастает до /Я, тах = Ми/(кФт1п) (линия Г на рис. 5.28, а).

5.4. Адаптивное управление в электроприводах

Рассмотренные способы управления с модальным и подчиненным регулированием координат электропривода распространяются на линейные объекты управления с заранее известными и неизменными параметрами. При изменении параметров нарушаются условия оптимизации, заложенные при синтезе соответствующих регуляторов, и динамические показатели электропривода ухудшаются. Особенно чувствителен к изменениям параметров способ подчиненного регулирования, который основывается на принципе компенсации больших постоянных времени. Для сохранения показателей качества электропривода в условиях изменяемости его параметров возникает задача адаптации, т.е. приспосабливаемое™ к данным условиям. Эта задача решается автоматическим путем - изменением параметров регуляторов, а также формированием дополнительных воздействий к действиям регуляторов [4].

Можно выделить два типа непостоянства параметров: параметр электропривода в исследуемом режиме остается неизменным или изменяется незначительно, но неизвестно его исходное значение;

параметр электропривода в исследуемом режиме существенно изменяется относительно его известного или неизвестного исходного значения.

К изменяемым параметрам электропривода могут быть отнесены:

момент инерции из-за изменения массы груза в подъемно-транспортных установках, взаимосвязи механических координат в многокоординатных манипуляторах и роботах;

индуктивность в цепях возбуждения с насыщением магнитной системы;

коэффициент усиления в управляемых преобразователях из-за изменения энергетического уровня источника питания;

активное сопротивление в силовых цепях из-за изменения температурного режима.

Кроме отмеченных изменяемых параметров на показатели качества электропривода может оказывать влияние и изменяемое возмущающее воздействие, к которому может быть отнесен труднодоступный измерению момент нагрузки.

В теории автоматического управления наиболее детально разработаны беспоисковые адаптивные системы управления (БАС) применительно к различным стационарным и квазистационарным объектам управления [15], в том числе и к электромеханическим системам [2, 4]. В данном типе БАС выделяются два класса:

БАС с эталонной моделью в виде динамического звена с желаемой динамикой (АСЭМ) (рис. 5.29, а);

0 ... 20 21 22 23 24 25 26 ... 49